Расстояние единственности

Стойкость криптосистемы, не зависящую от мощности вычислительных средств оппонента, можно оценить и по-другому, основываясь на неопределенности дешифрования при неизвестном ключе.

Будем считать, что оппоненту известна криптограмма E и описание системы шифрования/дешифрования симметричной криптосистемы, т.е. ему известны функции f (M,K), g (E,K) и ключевое пространство, но неизвестен конкретно использованный ключ K. Применяя к принятой криптограмме E силовую атаку (brute-force), т.е. перебирая все возможные элементы ключевого пространства, к которому принадлежит и истинный ключ K, можно попытаться восстановить сообщение. Еще раз отметим, что среди множества всех кандидатов на роль ключа только один является истинным, т.е. ключом, использованным при шифровании, тогда как остальные – ложные. Отбраковку кандидатов можно выполнять, используя критерий, основанный на получении в процессе перебора ключей осмысленного текста.

Однако может оказаться, что одной и той же криптограмме будут соответствовать несколько осмысленных расшифровок. В этом случае даже при неограниченной вычислительной мощности оппонента нет способа найти истинный ключ и восстановить истинное сообщение, зашифрованное в этой криптограмме.

Пусть одной и той же криптограмме соответствует S осмысленных расшифровок. Очевидно, что одна из них будет истинной расшифровкой, остальные S _Л.Р = _. S – 1 будут ложными. Тогда, если удастся построить криптосистему, которая для каждой криптограммы дает весьма большое число ложных расшифровок, то ее также можно будет считать стойкой, поскольку при любой вычислительной мощности оппонент не сможет определить, какая из допустимых осмысленных расшифровок является истинной.

Известно, что нижняя граница для среднего числа ложных расшифровок при фиксированной длине ключа N с ростом длины принятой криптограммы n падает. Когда она приблизится к нулю, можно считать, что ложных расшифровок не будет вообще. При длине криптограммы , где – длина криптограммы, обращающая в нуль нижнюю границу для среднего числа ложных расшифровок, всякая криптограмма, по-видимому, может быть рассекречена единственным образом, а при n < n ₀ это не так. Величина дает ту минимальную длину криптограммы, начиная с которой, ложные расшифровки будут отсутствовать и, следовательно, при переборе всех ключей каждой криптограмме будет соответствовать единственная осмысленная расшифровка, т.е. сообщение, которое в действительности и передавалось. Такая длина криптограммы называется расстоянием единственности n _Р.Е. = .

Важный вывод, справедливый для любых криптосистем, состоит в том, что, если оппонент перехватил криптограмму длины 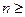n _Р.Е , то он всегда может без знания ключа дешифровать ее единственно правильным образом.

Анализ показывает: чем менее избыточным является источник, тем больше оказывается расстояние единственности. Для реальных сообщений с избыточностью и при относительно небольшой длине ключа, величина расстояния единственности n _Р.Е оказывается вполне приемлемой мерой, чтобы ответить на вопрос о стойкости криптограммы.

Например, для русскоязычного текста при двоичном ключе длиной N = 128 символов расстояние единственности составляет почти 40 букв. Это означает, что шифрование сообщений, содержащих менее 40 букв, является стойким по отношению к тотальному перебору ключей, а более длинные шифртексты вскрываются однозначно.

В заключение следует сделать общий вывод о том, что стойкие системы шифрования, криптоанализ которых не зависит от вычислительных или аппаратных возможностей оппонента, к сожалению, на коротких ключах (N << n) не реализуемы.

Дата добавления: 2015-10-26