Идеально стойкие криптосистемы

Существуют два основных класса стойкости криптосистем:

· Идеально (безусловно) стойкие или совершенные криптосистемы, для которых стойкость к криптоанализу (дешифрованию без знания ключа) не зависит от вычислительной мощности оппонента. Их называют теоретически недешифруемыми (ТНДШ) системами.

· Вычислительно стойкие криптосистемы, у которых стойкость к криптоанализу зависит от вычислительной мощности оппонента.

Система является теоретически не дешифруемой, если никакая криптограмма 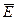при условии, что ключ 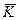неизвестен, не раскрывает никаких сведений о сообщении 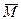, зашифрованном в эту криптограмму. В соответствие с теорией информации это происходит при условии, что равна нулю взаимная информация между множеством сообщений и множеством криптограмм. Из этого условия следует, что при неизвестном ключе дешифрования вероятность угадывания переданного сообщения не зависит от того, используется криптограмма или нет.

Оппоненты имеют доступ к открытому каналу связи и перехватывают, подслушивая, все криптограммы сообщений, которые пересылаются от отправителя к получателю. Но при идеальном шифровании, если оппоненты ничего не знают о ключе, криптосистема «обрывает» канал передачи от информации, которой обмениваются легальные пользователи, к оппонентам.

Равносильное определение идеального шифрования устанавливает независимость элементов любой пары 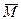и 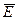из множества сообщений и множества криптограмм. Независимость означает, что перехват криптограммы не влияет на возможность расшифровки сообщения.

Можно показать, чтоесли двоичные элементы ключа выбираются взаимно независимыми и равновероятными, то этого достаточно, чтобы система шифрования оказалась ТНДШ.

Рассмотрим пример построения теоретически недешифруемой системы (рис. 2).

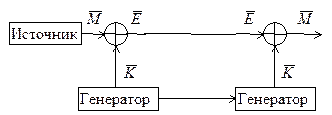  Рис. 2. Система передачи с шифрованием двоичных сообщений

Предположим (не умаляя общности), что сообщение является двоичной последовательностью 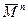длины n. Тогда можно сформировать криптограмму как двоичную последовательность такой же длины n по следующему правилу:

,

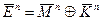используя поразрядное сложение 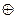по модулю 2 сообщения 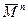с ключом 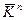. Здесь ключ также является двоичной последовательностью длины n и играет роль маскирующего слагаемого. Например, при n = 21 получаем

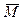
Å		Å
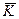
	,	010011110101100110101.
¾¾¾¾¾		¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾.

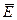
При известном ключе 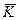, который должен быть передан на приемную сторону каким-либо секретным образом, сообщение легко восстанавливается по той же формуле, по которой производилось шифрование:

,

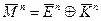поскольку .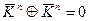

Дата добавления: 2015-10-26