Идеи и методы криптографии

3.1. Модели шифрования/дешифрования дискретных сообщений

В данном учебном пособии, как правило, рассматриваются вопросы, связанные с шифрованием и дешифрованием так называемых дискретных сообщений. Дискретные сообщения могут быть представлены сигналами с конечным числом состояний. К ним относятся данные, печатные тексты, а также речевые сигналы и изображения, если они предварительно преобразованы в дискретные (цифровые) сигналы. Для аналоговых сигналов используют другие методы защиты данных. Они будут рассмотрены отдельно.

Математической моделью системы шифрования/дешифрования дискретных сообщений называется пара функций

, ,

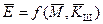которые преобразуют сообщение 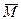в криптограмму 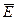при помощи ключа шифрования 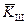и, наоборот, криптограмму 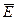в сообщение 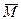при помощи ключа дешифрования . Обе функции, задающие криптосистему, должны удовлетворять следующим требованиям:

· Функции и при известных аргументах вычисляются сравнительно просто.

· Функция g (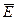,?) при неизвестном ключе дешифрования вычисляется достаточно сложно.

Голландский криптограф А. Керкхофс (1835 – 1903) предположил, что секретность шифров должна основываться только на секретности ключа, а не на секретности алгоритма шифрования, который, в конце концов, может оказаться известным противнику. Достоинство такого подхода несомненно: открытое опубликование алгоритма шифрования позволяет многим специалистам принять участие в анализе и обсуждении его свойств, стойкости и возможности технического применения. При рассмотрении современных систем шифрования предполагается, что ключ дешифрования неизвестен нелегальным пользователям (посторонним наблюдателям, оппонентам), хотя они и могут знать функции и , а также ключ шифрования 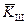, если он не совпадает с ключом дешифрования .

Следует различать три основных вида нападений (атак) оппонентов на криптосистему с целью узнать сообщение (в обобщенной постановке задачи, раскрыть ключ шифрования/дешифрования):

· Атака при известной криптограмме .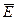

· Атака при известной криптограмме 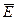и известном сообщении , которое соответствует определенной части криптограммы, полученной при использовании того же самого ключа (атака при частично известном открытом сообщении).

· Атака при известной криптограмме и специально выбранной части сообщения, соответствующей части криптограммы, полученной на том же ключе (атака с частично выбранным открытым сообщением).

Современные криптосистемы считаются стойкими, если они стойки относительно атак всех трех видов.

Для криптосистем, которые шифруют сообщения с невысокими требованиями к вероятности ошибки при передаче (цифровая речь, цифровое изображение) необходимо добавить четвертое, дополнительное, требование:

· Дешифрование после передачи криптограммы по каналам с помехами не должно увеличивать число ошибок по сравнению с тем числом ошибок, которые образовались в канале связи из-за помех, иными словами, не должно происходить размножение ошибок после дешифрования.

Если ключ шифрования равен ключу дешифрования, т.е.

= = ,

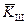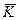то система называется симметричной (одноключевой). Для ее работы в пункты шифрования и дешифрования должны быть секретным образом доставлены одинаковые ключи .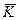

Если , т.е. ключ шифрования не равен ключу дешифрования, то система шифрования называется несимметричной (двухключевой). В этом случае ключ 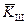доставляется в пункт шифрования, а ключ – в пункт дешифрования. Оба ключа очевидно должны быть связаны функциональной зависимостью j , но такой, что по известному ключу шифрования 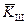нельзя было бы восстановить ключ дешифрования . Это означает, что для несимметричной системы шифрования функция j () должна быть трудно вычисляемой.

В несимметричной системе шифрования имеется возможность распределять среди законных пользователей секретным образом только их личные ключи дешифрования, а ключи шифрования сделать открытыми и опубликовать, например, в общедоступном справочнике. Поэтому такие криптосистемы называют системами с открытым (общедоступным) ключом. Криптосистема с общедоступным ключом (Public key cryptosystem) была впервые предложена Диффи и Хелманом в 1976 году.

В первой части курса будут рассмотрены только одноключевые (симметричные) системы.

Дата добавления: 2015-10-26