Необходимое условие теоретической недешифруемости

Практическим примером теоретически недешифруемой системы является система шифрования с одноразовым блокнотом. Блокнот выпускается в двух идентичных экземплярах для отправителя и получателя, имеет отрывные страницы, на которых напечатаны таблицы символов ключа. При шифровании и дешифровании значение символа ключа K_i определяется по местоположению соответствующего символа сообщения M_i или шифртекста E_i. Для каждого следующего символа сообщения или шифртекстаберется следующий символ из блокнота.

Каждое новое сообщение шифруется с новой страницы. Использованные страницы уничтожаются.

Заметим, однако, что рассмотренная система обладает существенным недостатком. Он заключается в том, что требуемая длина ключа N должна быть равна длине сообщения n:

N = n.

При передаче длинных сообщений необходима генерация, передача, и хранение в секрете огромного числа бит ключа. Это делает рассматриваемую систему дорогой и непригодной для массового применения, доступной разве только привилегированным пользователям. Более того, пока не доказано, что условие n = N, будучи достаточным, является и необходимым для построения любой ТНДШ.

Формулировка необходимого условия ТНДШ рассматривает не отдельные символы, а целые сообщения и выглядит следующим образом: число возможных ключей, используемых в теоретически не дешифруемых (ТНДШ) системах, должно быть не меньше числа сообщений, которые засекречиваются на этих ключах.

Полученный вывод может быть сформулирован и по-другому. Необходимым условием ТНДШ является пропорциональность длины ключа длине сообщения, поскольку, чем больше длина последовательности, тем больше существует для нее вариантов.

Из теории информации известно, что при 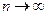все последовательности, выдаваемые источником сообщений делятся на два множества: множество типических и множество нетипических последовательностей. С вероятностью близкой к единице источник формирует только типические последовательности. Суммарная вероятность нетипических последовательностей практически равна нулю, и шифровать их, прямой необходимости нет. Шифровать нужно только, так называемые, «типические» последовательности. Тогда вариантов ключей может быть меньше, и ключи могут быть короче.

Более того. Из теории информации известно, что естественные источники (например, разговорные языки) обладают избыточностью. Обычно они производят число символов, несущих информацию, больше, чем необходимо для передачи этой информации. Поэтому для обеспечения наиболее экономного, с точки зрения длины ключа, идеального шифра первоначально выполняется кодирование, устраняющее избыточность (для документов это может быть представлено как архивирование), и лишь затем производится шифрование – сложение по модулю 2 ключевой последовательности со сжатым (более коротким) сообщением.

Таким образом, необходимым условием ТНДШ является пропорциональность длины ключа длине сообщения. Для избыточных источников коэффициент пропорциональности может быть уменьшен.

Дата добавления: 2015-10-26