Особенности асимметричных криптосистем

Асимметричная криптосистема – это такая криптосистема, в которой ключ шифрования K _Ш = K не совпадает с ключом дешифрования K _Д = k, т.е. k ¹ K, причем

E = f_K (M) = E_K (M), M = g_k (E) = M_k (E).

В дальнейшем для обозначения ключей шифрования и дешифрования в асимметричных криптосистемах будем использовать прописную и строчную букву: K и k.

Эти системы, имеющие еще одно название в связи со способом их применения – криптосистемы с открытым ключом, были предложены Диффи (W. Diffie) и Хеллманом (V. Hellman) в 1976 году.

Сформулируем основные требования, которым должна удовлетворять практически реализуемая криптосистема с открытым ключом:

Вычисление пары ключей K и k должно быть просто решаемой задачей при наличии некоторых данных, известных центру распределения ключей (ЦРК).

При известном ключе шифрования K вычисление криптограммы E = f_K (M) должно быть достаточно простым.

При известном ключе дешифрования k восстановление сообщения M = g_k (E) должно быть достаточно простым.

При известном ключе шифрования K вычисление ключа дешифрования k должно быть весьма сложным.

При известном ключе шифрования K, но неизвестном ключе дешифрования k, вычисление сообщения M по известной криптограмме E должно быть весьма сложным.

Если условие 4 выполнено, то, очевидно, что ключ шифрования K можно сделать открытым и при этом стойкость системы не нарушится. Именно вследствие этого и появилось название таких криптосистем. Однако, чтобы показать, что асимметричные криптосистемы имеют смысл, необходимо дать ответы на следующие два вопроса:

Зачем нужны криптосистемы с открытым ключом, если существуют достаточно стойкие симметричные криптосистемы (блоковые или потоковые)? Каковы их преимущества перед обычными системами?

Существуют ли вообще асимметричные системы шифрования, удовлетворяющие основным требованиям?

Попытаемся дать ответы на эти вопросы.

Основное преимущество асимметричных систем шифрования с открытым ключом состоит в том, что они существенно упрощают проблему распределения ключей в сети с большим числом пользователей.

Действительно, пусть имеется n пользователей, каждый из которых хочет вести переговоры с любым другим секретно от остальных, используя симметричную криптосистему. В этом случае каждый пользователь должен получить и хранить в секрете n – 1 ключ, а общее число секретных ключей в сети, генерируемых и распределяемых ЦРК, должно составлять 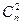= n (n – 1)/2.

Если же использовать асимметричные криптосистемы, то все пользователи должны получить от ЦРК только по одному секретному ключу дешифрования k_i, i = 1, 2,…, n, в то время как соответствующие ключи шифрования K_i могут быть помещены в открытый справочник, доступный для всех. Тогда, если пользователь A хочет переслать сообщение пользователю B, то он находит в справочнике открытый ключ шифрования пользователя B, формирует криптограмму и пересылает ее по открытому каналу связи. Пользователь B с помощью своего секретного ключа дешифрования восстанавливает сообщение . Схема обмена сообщениями между пользователями A и B показана на рис. 17.

Рис. 17. Обмен сообщениями в двухключевой криптосистеме

Второе преимущество асимметричных систем по сравнению с симметричными системами состоит в том, что они, помимо функции шифрования/дешифрования, могут реализовывать и ряд других дополнительных функций, например цифровую подпись.

Наконец, третьим преимуществом является то, что асимметричные системы имеют более «прозрачный» криптоанализ (т.е. проще оценивается стойкость конкретной системы), поскольку, как будет показано в дальнейшем, их криптостойкость базируется на сложности решения четко сформулированных математических задач.

Однако в асимметричных криптосистемах приходится использовать более длинные ключи и процедура шифрования/дешифрования совершается медленнее. В таблице сопоставлена длина ключей симметричных и асимметричных криптосистем при одинаковом уровне секретности.

Длина ключа в битах
симметричной криптосистемы	асимметричной криптосистемы

Дата добавления: 2015-10-26