Основні алгоритми теорії потоків

Алгоритми визначення максимального потоку

На підставі властивостей двоїстості задач лінійного програмування, як це показано в попередніх розділах, можливо визначити максимальний потік в мережі. Однак більш простішим є алгоритм Форда-Фалкерсона.

Розглянемо алгоритм отримання максимального потоку з любого початкового потоку. Ця процедура складається з двох операцій: операції А – процесу розташування поміток в вершинах мережі (графу) і операції В – зміни потоку. В наявності є кілька модифікацій методу поміток, в які закладена одна і та ж ідея: шляхом певної системи поміток визначаються ланцюги (шляхи), які не містять насичених дуг. Помітка починається з джерела (початку) х₀, яка помічається індексом 0, тобто . Нехай задана вже помічена вершина х_і (рис. 6). Якщо для деякої поміченої вершини х_і є суміжна вершина х_j, яка з’єднується з нею насиченою дугою, то остання вершина не помічається (рис. 6, а). Якщо слідуючи вершина з’єднана з поміченою х_і дугою зі значенням потоку , то вершина х_j помічається знаком +і, тобто (рис. 6, б).

Якщо вершина х_j пов’язана з х_і з позитивним нульовим потоком , то вона позначається знаком -і, тобто (рис. 6, в). Таким чином, не помічаються такі вершини, які з’єднані з поміченою суміжною вершиною х_і виходячи з неї насиченою дугою, або дугою з нульовим потоком, що входить в неї (рис. 6, г).

Ясно, що потік в мережі можна збільшити за рахунок збільшення потоків в дугах, що закінчуються вершинами, поміченими знаком "+" і зменшення потоків дугах, що закінчуються в вершинах, помічених знаком "–". На рис. 7 наведено приклад поміченого шляху.

Рис. 7. Приклад поміченого шляху

Припустимо, що процедурі помічення вершин, вдалося знайти такий шлях (всі вершини його помічені), що в нього попала кінцева вершина. Тоді така ситуація називається прорив (по одному із шляхів прорвалися до кінця). В протилежному випадку кажуть про не прорив. Це означає, що між початком х₀ і кінцем х_z є шлях , вершини якого помічені індексами попередніх вершин. Тоді можливо збільшити потік в мережі. Справді, так як знайдений шлях не містить в собі жодної прямої насиченої дуги, то можна змінити значення потоків на всіх дугах цього шляху на величину

,

причому потік на дузі збільшується на h, якщо орієнтація дуги співпадає з напрямком від х₀ до х_z і зменшується на в протилежному випадку. Після цього отримуємо новий потік, збільшений на величину h. Далі всі помітки на вершинах графу зтираються і процедура повторюється спочатку. Цей процес повторюють до тих пір, доки неможливо знайти жодного шляху , тобто до не прориву. На цьому останньому кроці ми отримуємо максимальний потік. Слід зауважити, що існують і інші форми запису алгоритму, наприклад [28]. Початкова вершина помічається . Суміжна наступна вершина х_j помічається , якщо

,

де . (2.1)

або ця вершина помічається , якщо , де

. (2.2)

Процедуру отримання максимального потоку рекомендується починати з нульового значення потоку.

Приклад. Визначимо максимальний потік в мережі, яка наведена на рис... Біля кожної дуги проставлена її пропускна спроможність. Послідовний процес розв’язку наводиться в таблиці.

Таблиця

Дуги

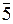
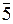
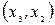
В цьому простому прикладі без особливої праці можна знайти шлях від х₀ до z, який не містить насичених дуг. Таким є шлях . У відповідності з формулою (2.1) збільшуємо значення потоку на дугах цього шляху на 2 тоді дуга стає насиченою (в табл. це відмічено рискою зверху). Відповідні значення потоку наведені в третьому стовпчику табл. На другій ітерації вибираємо другий шлях , вільний від насичених дуг.

Рис. 8 Пояснення до прикладу

Змінюємо (збільшуємо) значення потоку на . Сумарний потік наведений в четвертому стовпчику. На третій ітерації вибирається шлях 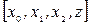, потік збільшується на 2. результати наведені в п’ятому стовпчику. Прорив з точки z більше ніяким чином здійснити неможливо. Отриманий потік є максимальним зі значенням Ф=7.

Приклад. Проілюструємо метод поміток вершин на прикладі мережі, що наведена на рис. 9, а. Джерелу х₀ надаємо мітку 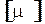. Далі, вершині х₂ надаємо мітку . Це єдина вершина, яку можна помітити, починаючи з х₀, тому що дуга (х₀, х₁) є насиченою. Продовжуючи процес з х₂ можемо помітити вершину х₁ двома способами: або . Настав прорив, рис. 9, б. Вздовж розглянутого шляху значення . Змінюємо на це значення потоки на дугах. Отримуємо новий потік зі значенням сумарного потоку на кінцевих дугах 2 (замість початкового, який дорівнював 1), який представлений на рис. 9, в. Далі знов проходить прорив вздовж шляху . Після зміни потоків на маємо потік, який наведений на рис. 9, г, з максимальним значенням потоку на кінцевих дугах 3. мінімальний розріз складається з дуг .

Рис. 9 Пояснення до прикладу.

Дата добавления: 2015-10-26