Стверджується, що кінцева вершина

z Î X. (1.20)

(1.21)

Доводиться це методом від зворотнього [29], припустимо, що це не так. Тоді із визначення множини Х витікає, що існує шлях з вершини x₀ в вершину Z, тобто

Який на рис. 4 має ту властивість, що для прямих дуг цієї мережі.

(1.22)

а для зворотних буде

Рис. 4. Пояснення до теореми про максимальний потік

Позначимо через e₁ мінімум різниці який береться по всім прямим дугам цього шляху, а через e₂ – мінімум по всім зворотнім дугам. Введемо величину . Змінимо потік j, збільшивши його на e на всіх прямих дугах шляху, тобто 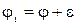і зменшивши його на цю величину на всіх зворотних дугах, тобто .

В цьому випадку величина сумарного потоку на кінцевих дугах мережі, яка була Ф складає

(1.23)

Але (1.23) суперечить тій умові, що потік в мережі j є максимальним. Таким чином (1.20) доведено, отже доведена теорема про максимальний потік.

З цього факту випливає важливий наслідок:

Потік j є максимальним в тому і тільки в тому випадку, якщо нема ні одного шляху, який збільшує його.

Цей наслідок дає ефективний засіб визначення максимального потоку. Для того, щоб потік зробити максимальним, необхідно наситити всі дуги розрізу .

Задачі теорії потоків і лінійного програмування

Для подальшого нам знадобляться знання про властивості прямої і двоїстої задачі лінійного програмування. Сформулюємо ці властивості в іншій формі, ніж вони звичайно розглядаються в дослідженні операцій [4, 5]. Наведемо ці властивості без доведення. Пряма задача формулюється таким чином. Потрібно визначити значення змінних , які задовольняють співвідношенням

(1.24)

і падають максимуму лінійній формі

(1.25)

Для подальшого важливо, що величина мають любі знаки, а величини 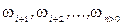(ці змінні відповідають нерівностям двоїстої задачі).

Цій прямій задачі ставиться у відповідність двоїста задача. При цьому кожному з обмежень (1.24) ставляться у відповідність двоїсті змінні і; для цих змінних складаються обмеження з рівностей і нерівностей

(1.26)

причому змінні мають довільні знаки, а змінні

(1.27)

Потрібно визначити такі значення змінних які б задовольняли умовам (1.26) і мінімізували форму

Коефіцієнти в лівій частині (1.26) отримуються транспонуванням матриці системи (1.24).

Вектор який задовольняє обмеженням основної задачі називається допустимим вектором, а основна задача - допустимою задачею. Допустимий вектор, який максимізує (1.25) називається оптимальним вектором, а задача - оптимальної. Така ж термінологія застосовується для двоїстої задачі.

Для кожної з цих задач можливі три випадки:

- є оптимальні вектори (а отже і допустимі);

- є допустимі вектори, але немає оптимальних;

- немає допустимих векторів.

(1.28)

Основна теорема двоїстості стверджує, що

Припустимо, що основна, а отже і двоїста задача має допустимі вектори.

(1.29)

Покажемо, що

Нехай w і l допустимі вектори, тоді

(1.30)

(1.31)

Тому що для тих змінних , які приймають значення любого знака, виконуються рівності

(2.31)

а для невід'ємних змінних справедливими є нерівності

(1.32)

Якщо якась j-та нерівність двоїстої задачі не обертається в точну рівність (є суворою нерівністю), тобто

то рівність в формулі (1.30) для допустимих рівнянь можлива тільки при умові, що відповідна j-та змінна основної задачі обертається в нуль, тобто .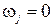

Ця вимога є необхідною і достатньою. Умовно це можна представити таким чином:

(1.33)

Це положення називають другою теоремою двоїстості [4, 5, 29] і формулюють таким чином. Для того, щоб допустимі розв'язки W і l пари двоїстих задач обертали в рівність співвідношення (1.30) тобто були оптимальними, необхідно і достатньо виконання наступної умови: якщо якась з нерівностей системи обмежень однієї задачі не обернулась в точку рівність то відповідна змінна іншої задачі повинна дорівнювати нулю. Аналогічним чином

(1.34)

тому що для тих змінних , які мають любий знак, справедливими є рівності

(1.35)

Якщо для деякого і в (1.35) виконується знак рівності, то необхідно і достатньо, щоб

Це положення умовно можна позначити таким чином:

(1.36)

Доведено наступні: для того, щоб допустимі розв'язки W і l пари задач обертали (1.34) в рівність (були оптимальними) необхідно і достатньо виконання наступної умови: якщо якась із змінних однієї з двоїстих задач суворо позитивна, то відповідне обмеження іншої (основної) задачі повинно обертатися в рівність. Із порівняння (1.30) і (1.34) виходить, що

(1.37)

Рівність в (1.37) можлива тоді і тільки тоді, коли виконуються умови (1.33) і (1.36).

Теорему про максимальний потік можна отримати з теореми двоїстості Теорема двоїстості, теорема про максимальний потік і теорема про мінімальне в теорії ігор – це різні формування одного і того ж положення. Розглянемо рівняння, які визначають максимальний потік, і складемо для них двоїсту задачу:

(1.38)

(1.39)

.

Неважко переконатися в тому, що матриця коефіцієнтів лівої частини співпадає з матрицею інциденцій.

Співставимо з равенствами (1.38) величини (всього їх N+2, де N – число внутрішніх вершин мережі), а нерівностям (1.39) – величини Нагадаємо, що

Тоді у відповідності з формальними правилами побудови двоїстої задачі отримаємо:

При цих обмеженнях потрібно знайти мінімум лінійної форми

(1.43)

Пояснимо це на прикладі

Приклад 3. неважко переконатися, що для мережі, яка зображена на рис. 5, матриця інциденцій має вигляд:

(1.44)

	(х0, x)	(х0, y)	(х, y)	(y, x)	(х, z)	(y, z)
х0
х	-1			-1
у		-1	-1
z					-1	-1

Рядки матриці інциденцій відповідають вершинам, стовпчикам, дугам. Якщо дуга виходить з вершини, то на перетині відповідних рядка і стовпчика стоїть +1, якщо входить, то стоїть –1. Коли вершини неінцедентні, тобто не є ні початковою ні кінцевою вершиною дуги, то ставиться нуль. Дамо пояснення до співвідношень (1.40) – (1.44). По-перше, так як лінійна форма основної задачі залежить від величини , включимо її в невідомі, перенесли в ліву частину в співвідношеннях (1.38) і добавив в матриці інциденцій відповідний стовпчик

Тоді матриця коефіцієнтів перепишеться в вигляді

	(х0, x1)	(х0, y)	(х, y)	(y, x)	(х, z)	(y, z)	φ
х0							-1
х	-1			-1
у		-1	-1
z					-1	-1

В останню матрицю добавлено шість рядків, які відповідають нести рівнянням­ – обмеженням на пропускну спроможність. Випишемо кілька рівнянь, які відповідають рівнянням (1.45) в розвернутому вигляді.

Для х = х₀ друга сума в (1.38) не дає ні одного члена;

Для х ≠ х₀, z друга сума дає два члени. Тоді (1.38) буде мати вигляд:

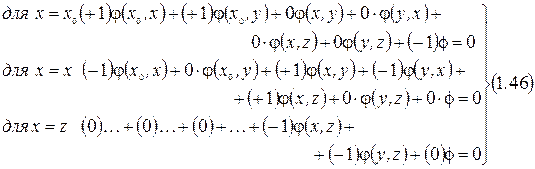
Якщо транспортувати матрицю (1.45) і врахувати, що відповідає першому рівнянню в (1.46), а – останньому, то отримаємо рівняння (1.40).

Одиниця в правій частині (1.40) стоїть тому, що відповідний коефіцієнт лінійної форми дорівнює одиниці.

Можна показати, що якщо – мінімальний розріз, який відділяє х₀ від z, то оптимальний розв’язок двоїстої задачі дається формулами

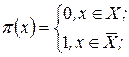(1.47)

(1.48)

Цікаво відмітити, що розв’язки (1.47) і (1.48) дають: розв’язок двоїстої задачі – мінімальний розріз, розв’язок прямої задачі – максимальний потік.

Дата добавления: 2015-10-26