Основні поняття та означення теорії потоків

Як говорилося вище, теорія потоків має справу з класом графів, які називаються транспортними мережами або просто мережами.

Скінчений граф (Х, Т) без петель називається сіткою, якщо кожній дузі 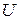співставлень у відповідальність ціле число яке називається пропускною спроможністю дуги. Цьому графу властиві наступні властивості:

1) існує одна і тільки одна вершина х₀, з якої дуги виходять, але ні одна не входить. Ця вершина називається входом або джерелом сітки;

2) існує одна і тільки одна вершина графа Z, в яку входять дуги, але ні одна дуга не виходить. Ця вершина називається виходом, або стоком сітки (мережі).

Для сіток вводять поняття потоку. Хай 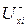множина дуг, які входять в вершину х_і, а 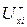– множина дуг, які виходять з вершини х_і. Функція , яка визначена на множині дуг сітки n і приймає цілочисельні позитивні значення, являє собою потік даної транспортної сітки, якщо

; (1.1)

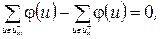
(1.2)

Перша умова означає, що потік дуги не може перевищувати її пропускну спроможність. Друга умова стверджує, що сумарний потік дуг, які входять в вершину, дорівнює сумарному потоку, який з вершини виходить (за виключенням точок входу і виходу). Інколи остання залежність називається умовою збереження потоку, тому що вона стверджує, що в любій проміжній точці потік не створюється і не щезає.

Ясно, що транспортні мережі, типа мережі автомобільних чи залізничних мереж, мережі ліній зв’язку (телеграфних, телевізійних, телефонних), задовольняють цим умовам і володіють потоком. Дуги можна інтерпретувати, як шляхи сполучення; пропускна спроможність дуги в цьому випадку можна сприймати як кількість одиниць потоку, який може бути пропущений по конкретній дузі в одиницю часу. В цьому випадку значення потоку на дузі являє собою кількість товарів, які дійсно перевозяться по дузі в одиницю часу.

Введемо поняття сумарного на кінцевих дугах сітки, яке відрізняється від поняття потоку на дузі . З (1.2) виходить, що сума потоків, які виходять з початкової вершини х₀ дорівнює сумі потоків, які входять в кінцеву вершину Z

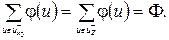(1.3)

Коли говорять, що на сітці заданий потік, то це означає, що задані дугові потоки 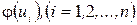, де n – кількість дуг в графі сітки.

Припустимо, що множина всіх вершин даної мережі розбито на дві взаємно доповнюючих множини , причому перша підмножина містить в собі вхід мережі , а друге – вихід мережі , тобто всі вершини мережі, які не ввійшли в підмножину Р, повинні міститися в підмножині .

В цьому випадку говорять, що в сітці проведений розріз.

Множина дуг 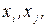де 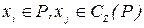, називається розрізом. Сума пропускних спроможностей дуг розрізу називається величиною розрізу і позначається Г або Г[Y, C(Y)]. В останньому позначенні вказують взаємні доповнюючи підмножини, які визначають розріз. Як правило, зі зміною розрізу змінюються і його значення.

В загальному випадку величини потоку на кінцевих дугах ніколи не перевищує величину розрізу

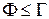(1.4)

Доведемо це співвідношення (хоча це логічно ясно). З формули (1.3) виходить, що

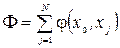(1.5)

Тут через позначається потік дуги, яка з’єднує вершини , причому вважається, що

(1.6)

якщо не існує дуги .

Загальна кількість вершин в мережі, не рахуючи входу і виходу, дорівнює N. Додамо до обох частин рівності (1.5) величину

(1.7)

де через Р-х₀ позначена одна з підмножин розрізу без початкової точки; – потік на дузі .

При цьому вважається, що потік тече в обидва боки, тобто ці вершини з’єднують пряма і зворотна дуга.

Величина (1.7) у відповідності до співвідношення (1.2) дорівнює нулю. В результаті отримаємо:

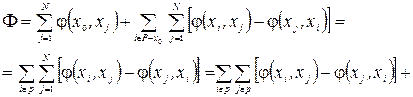
(1.8)

Тому що при фіксованому 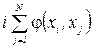дорівнює сумарному потоку, який виходить з вершини і, а 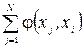– сумарному потоку, який входить в вершину і.

Перший доданок в останній частині (1.8) дорівнює нулю, тому що всі його доданки взаємно знищуються. Отже,

(1.9)

Тут використана на умові, згідно якої, значення потоку на дузі не перевищує її пропускної спроможності

. (1.10)

В зв’язку з тим, що реальний потік не може бути від’ємним, то за позитивний напрямок приймають напрямок більшого потоку. Вираз (1.10) означає, що дві дуги в протилежних напрямках між двома вершинами можна замінити однією, потік в якій визначається за допомогою (1.10).

1.1.3. Теорема про максимальний потік (теорема Форда-Фалкерсона)

Фордом і Фалкерсоном доведена фундаментальна теорема, яка має дуже велике значення в теорії графів, яка стверджує, що в любій мережі максимальне значення сумарного потоку на кінцевих дугах дорівнює мінімальній пропускній спроможності розрізу.

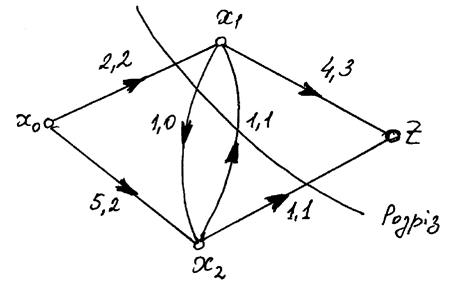
Рис. 2. Пояснення до прикладу 2.1.

Приклад 2.1. На рис. 2 наведена мережа, яка складається з чотирьох вершин і шести дуг. На кожній дузі проставлена її пропускна спроможність (перша цифра) і потік (друга цифра). З малюнку видно, що для проміжних вершин х₁ і х₂ умови збереження потоку виконуються, Ф=4. Можна знайти розріз, пропускна спроможність якого Г=4. Цей розріз складається з дуг (х₀, х₁), (х₂, х₁), (х₂, х_z). Дуга (х₁, х₂) в розріз не входить.

Потік на кінцевих дугах – максимальний, а пропускна спроможність розміру – мінімальна. Наприклад, пропускна спроможність розрізу 1 – Г=5, а розрізу 2 – Г=10.

Розглянемо доведення теореми про максимальний потік. Необхідно знайти такий розріз

, щоб для

(1.11)

(1.12)

Співвідношення (1.12) можна пояснити таким чином. Ясно, що максимальний потік в розрізі буде тоді, коли в нього поперед всього включаються пари вершин, які або не мають зворотних дуг, або мають нульове значення потоку по зворотній дузі (рис. 2), тому що любе значення потоку по зворотній дузі зменшує сумарний потік між двома вершинами і він не буде максимальним.

Якщо ввести позначення

(1.13)

(1.14)

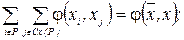(1.15)

то вважаючи, що Х=Р, а , співвідношення (1.11) і (1.12) можна переписати у вигляді

(1.16)

(1.17)

Якщо для вибраного максимального потоку буде знайдений розріз з такими властивостями, то теорема про максимальний потік буде доведена. Максимальний потік j* в мережі завжди існує, тому що значення дугового потоку завжди обмежене і дискретне, отже, існує скінчений набір значень потоку в мережі (при скінченій кількості дуг). З яких завжди можна вибрати по крайній мірі одне максимальне значення потоку в мережі.

Вважаючи, що максимальний потік в мережі φ* заданий, визначимо множину Х наступним рекурентним чином:

(1.18)   (1.19)

Проаналізуємо процедуру (1.19). В мережі, на дугах якої задані максимальні потоки, виділимо під мережу, виключив прямі дуги (х, у), де потоки досягають максимальних значень, що дорівнюють пропускним спроможностям С (х, у). На рис. 3 наведені можливі локальні структури мережі.

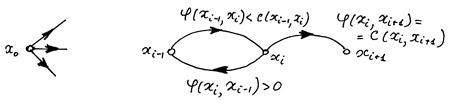
Рис. 3. Локальні структури мережі

На рис. 3а показано вхід мережі. На рис. 3 б, в, г показані внутрішні ділянки мережі, які з'єднують вершини. У відповідності до правил (1.19) дуга (х_і, Х_і+1) на рис. 3 б виключається і вершина Х_і+1 не попадає в множину X; вершина Х₂ на рис. 3 в, не попадає, а вершина Х₄ - попадає в множину X, тому що Х₃ є Х.

Дата добавления: 2015-10-26