
Читайте также:
|
Задания на контрольную работу
Задание 1
Вариант 1
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023; 789,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2; 98С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101; 110011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
11001101,101 + 11001101,1011=?
б) EF567,AD6 + 678ADE,567 =?
AD678,C678 + 456AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
б) 1101,11*101,1 =?
Вариант 2
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025; 729,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2; 9АС84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001; 100011,111
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
1101111,101 + 1100001,1011=?
б) EF567,AВ + 678A4E,567 =?
AD674C,68 + 49AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
б) 1001,11*1011,1 =?
Вариант 3
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023; 589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант 4
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
234,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2; ААС34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101; 111001,101
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
11111101,101 + 11101,1101,1011=?
б) EFВ47,AD6 + 634ADE,577 =?
A7В78,C678 + 672AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
б) 1101,11*110,1 =?
Вариант 5
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
569,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2; 97С84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001; 101011,111
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
1100001,101 + 1011001,1011=?
б) EF597,AВ + 438A4E,567 =?
AD574C,68 + 78AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
б) 1111,11*10001,1 =?
Вариант 6
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант 7
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
789,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2; 98С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101; 110011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
11001101,101 + 11001101,1011=?
б) EF567,AD6 + 678ADE,567 =?
AD678,C678 + 456AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
б) 1101,11*101,1 =?
Вариант 8
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
729,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2; 9АС84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001; 100011,111
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
1101111,101 + 1100001,1011=?
б) EF567,AВ + 678A4E,567 =?
AD674C,68 + 49AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
б) 1001,11*1011,1 =?
Вариант 9
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант 10
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
234,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2; ААС34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101; 111001,101
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
11111101,101 + 11101,1101,1011=?
б) EFВ47,AD6 + 634ADE,577 =?
A7В78,C678 + 672AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
б) 1101,11*110,1 =?
Вариант 11
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
569,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2; 97С84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001; 101011,111
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
1100001,101 + 1011001,1011=?
б) EF597,AВ + 438A4E,567 =?
AD574C,68 + 78AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
б) 1111,11*10001,1 =?
Вариант 12
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант 13
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
789,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2; 98С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101; 110011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
11001101,101 + 11001101,1011=?
б) EF567,AD6 + 678ADE,567 =?
AD678,C678 + 456AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
б) 1101,11*101,1 =?
Вариант14
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
729,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2; 9АС84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001; 100011,111
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
1101111,101 + 1100001,1011=?
б) EF567,AВ + 678A4E,567 =?
AD674C,68 + 49AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
б) 1001,11*1011,1 =?
Вариант15
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант16
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
234,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2; ААС34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101; 111001,101
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
11111101,101 + 11101,1101,1011=?
б) EFВ47,AD6 + 634ADE,577 =?
A7В78,C678 + 672AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
б) 1101,11*110,1 =?
Вариант17
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
569,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2; 97С84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001; 101011,111
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
1100001,101 + 1011001,1011=?
б) EF597,AВ + 438A4E,567 =?
AD574C,68 + 78AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
б) 1111,11*10001,1 =?
Вариант18
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант19
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
789,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2; 98С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101; 110011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
11001101,101 + 11001101,1011=?
б) EF567,AD6 + 678ADE,567 =?
AD678,C678 + 456AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
б) 1101,11*101,1 =?
Вариант20
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
729,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2; 9АС84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001; 100011,111
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
1101111,101 + 1100001,1011=?
б) EF567,AВ + 678A4E,567 =?
AD674C,68 + 49AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
б) 1001,11*1011,1 =?
Вариант21
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант22
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
234,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2; ААС34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101; 111001,101
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
11111101,101 + 11101,1101,1011=?
б) EFВ47,AD6 + 634ADE,577 =?
A7В78,C678 + 672AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
б) 1101,11*110,1 =?
Вариант23
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
569,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2; 97С84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001; 101011,111
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
1100001,101 + 1011001,1011=?
б) EF597,AВ + 438A4E,567 =?
AD574C,68 + 78AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
б) 1111,11*10001,1 =?
Вариант24
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант25
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
345,0023;
789,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ673,Е2; 98С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1001101.1101; 110011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100111,1101 + 11110011,1101=?
11001101,101 + 11001101,1011=?
б) EF567,AD6 + 678ADE,567 =?
AD678,C678 + 456AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11011,101* 1001,101 =?
б) 1101,11*101,1 =?
Вариант26
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
641,0025;
729,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС873,Е2; 9АС84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1101101.1001; 100011,111
4. Произвести сложение с проверкой вычитанием:
а) 1010111,1011 + 11001111,10101=?
1101111,101 + 1100001,1011=?
б) EF567,AВ + 678A4E,567 =?
AD674C,68 + 49AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 10011,101* 1101,101 =?
б) 1001,11*1011,1 =?
Вариант27
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Вариант28
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
567,0023;
234,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АВ233,Е2; ААС34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
110011.1101; 111001,101
4. Произвести сложение с проверкой вычитанием:
а) 11010111,1101 + 11001011,1101=?
11111101,101 + 11101,1101,1011=?
б) EFВ47,AD6 + 634ADE,577 =?
A7В78,C678 + 672AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 101011,101* 1101,101 =?
б) 1101,11*110,1 =?
Вариант29
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
941,0025;
569,791
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
АС8433,Е2; 97С84,А9
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1100001.1001; 101011,111
4. Произвести сложение с проверкой вычитанием:
а) 1011111,1011 + 110010111,10101=?
1100001,101 + 1011001,1011=?
б) EF597,AВ + 438A4E,567 =?
AD574C,68 + 78AEА,45 =?
5. Произвести умножение двоичных чисел:
а) 11100,101* 1101,101 =?
б) 1111,11*10001,1 =?
Вариант30
1. Выполнить последовательный перевод данных (десятичных) чисел
в двоичную и шестнадцатеричную системы счисления:
745,0023;
589,761
2. Выполнить последовательный перевод данных (шестнадцатеричных) чисел
в двоичную и десятичную системы счисления:
9В673,Е2;198С34,А3
3. Выполнить последовательный перевод данных (двоичных) чисел
в шестнадцатеричную и десятичную системы счисления:
1011101.1101; 100011,101
4. Произвести сложение с проверкой вычитанием:
а) 1100101,1101 + 11010011,1101=?
11011101,101 + 11011101,1011=?
б) 8F567,AD6 + 238ADE,567 =?
AD670,C678 + 956AECD,945 =?
5. Произвести умножение двоичных чисел:
а) 11111,101* 1001,001 =?
б) 1001,11*111,1 =?
Задание 2
Вариант 1
1. Составить схему алгоритма и программу, вычисляющую заданный интеграл по формулам прямоугольников, трапеций или Симпсона. Найти наименьшее значение n, при котором каждая из формул дает приближенное значение интеграла с погрешностью, не превышающей eps. Вычислить погрешность по правилу Рунге.
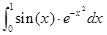 ,eps=0,0001.
,eps=0,0001.
2. Отделить корни уравнения x3-3x2+9x-8=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
Вариант 2
1. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
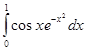 , eps=0,0001
, eps=0,0001
2. Отделить корни уравнения х - sinx = 0.25 графически и уточнить один из них методом простых итераций с точностью до 0,001
Вариант 3
1. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
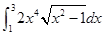 ,eps=0,0001.
,eps=0,0001.
2. Методом наименьших квадратов найти квадратичную зависимость для экспериментальных данных, приведённых в таблице. В одной и той же системе координат изобразить график функции и точки.
| x | 4.5 | 5.0 | 5.5 | 6,0 | 6.5 |
| y | 7.7 | 9.4 | 11.4 | 13.6 | 15.6 |
Вариант 4
1. Решить систему нелинейных алгебраических уравнений методами Зейделя или простой итерации, точность данных методов e= 0,001
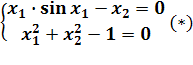
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 5
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Составить таблицу заданных конечных сумм. Размер сумм определены либо количеством членов N, либо требуемой точностью вычислений 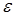 . В последнем случае добавление новых членов следует прекратить, если
. В последнем случае добавление новых членов следует прекратить, если 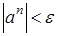 . Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
. Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
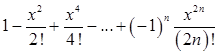
Вариант 6
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
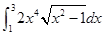 ,eps=0,0001.
,eps=0,0001.
Вариант 7
1. Найти действительный корень уравнения, лежащего в интервале [0.1;0.125] с точностью 10-4:
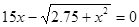
2. Решить систему линейных уравнений с точностью 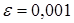
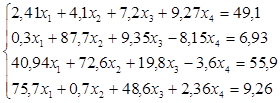 ,
,
Вариант 8
1. Отделить корни уравнения 2x4+3x3+5x2-18=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
2. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
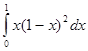
Вариант 9
1.
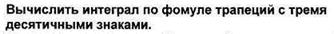
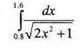
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 10
1.

Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 11
1. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
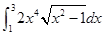 ,eps=0,0001.
,eps=0,0001.
2. Методом наименьших квадратов найти квадратичную зависимость для экспериментальных данных, приведённых в таблице. В одной и той же системе координат изобразить график функции и точки.
| x | 4.5 | 5.0 | 5.5 | 6,0 | 6.5 |
| y | 7.7 | 9.4 | 11.4 | 13.6 | 15.6 |
Вариант 12
1. Для уравнения x2+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
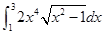 ,eps=0,0001.
,eps=0,0001.
Вариант 13
1. Составить таблицу заданных конечных сумм. Размер сумм определены либо количеством членов N, либо требуемой точностью вычислений 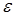 . В последнем случае добавление новых членов следует прекратить, если
. В последнем случае добавление новых членов следует прекратить, если 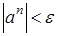 . Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
. Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
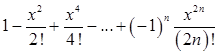
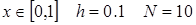
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
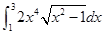 ,eps=0,0001.
,eps=0,0001.
Вариант 14
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
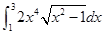 ,eps=0,0001.
,eps=0,0001.
Вариант 15
1. Составить схему алгоритма и программу, вычисляющую заданный интеграл по формулам прямоугольников, трапеций или Симпсона. Найти наименьшее значение n, при котором каждая из формул дает приближенное значение интеграла с погрешностью, не превышающей eps. Вычислить погрешность по правилу Рунге.
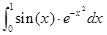 ,eps=0,0001.
,eps=0,0001.
2. Отделить корни уравнения x3-3x2+9x-8=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
Вариант 16
1. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
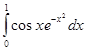 , eps=0,0001
, eps=0,0001
2. Отделить корни уравнения х - sinx = 0.25 графически и уточнить один из них методом простых итераций с точностью до 0,001
Вариант 17
1. Найти действительный корень уравнения, лежащего в интервале [0.1;0.125] с точностью 10-4:
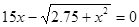
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
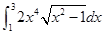 ,eps=0,0001.
,eps=0,0001.
Вариант 18
1. Отделить корни уравнения 2x4+3x3+5x2-18=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
2.Составить программу, вычисляющую заданный интеграл по формуле Гаусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
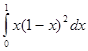
Вариант 19
1.
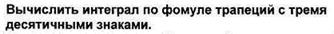
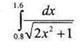
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 20
1.

Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 21
1. Составить схему алгоритма и программу, вычисляющую заданный интеграл по формулам прямоугольников, трапеций или Симпсона. Найти наименьшее значение n, при котором каждая из формул дает приближенное значение интеграла с погрешностью, не превышающей eps. Вычислить погрешность по правилу Рунге.
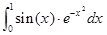 ,eps=0,0001.
,eps=0,0001.
2. Отделить корни уравнения x3-3x2+9x-8=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
Вариант 22
1. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
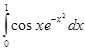 , eps=0,0001
, eps=0,0001
2. Отделить корни уравнения х - sinx = 0.25 графически и уточнить один из них методом простых итераций с точностью до 0,001
Вариант 23
1. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
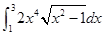 ,eps=0,0001.
,eps=0,0001.
2. Методом наименьших квадратов найти квадратичную зависимость для экспериментальных данных, приведённых в таблице. В одной и той же системе координат изобразить график функции и точки.
| x | 4.5 | 5.0 | 5.5 | 6,0 | 6.5 |
| y | 7.7 | 9.4 | 11.4 | 13.6 | 15.6 |
Вариант 24
1. Решить систему нелинейных алгебраических уравнений методами Зейделя или простой итерации, точность данных методов e= 0,001
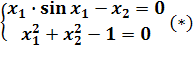
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 25
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Составить таблицу заданных конечных сумм. Размер сумм определены либо количеством членов N, либо требуемой точностью вычислений 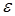 . В последнем случае добавление новых членов следует прекратить, если
. В последнем случае добавление новых членов следует прекратить, если 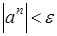 . Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
. Необходимо проделать анализ полученной таблицы, выявить наибольшее отклонение в таблице от точного значения и составить рекомендации по использованию конечных сумм.
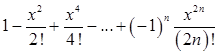
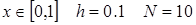
Вариант 26
1. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
2. Вычислить интеграл формулам прямоугольников, трапеций или Симпсона с двумя десятичными знаками. Для оценки погрешности использовать правило Рунге.
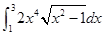 ,eps=0,0001.
,eps=0,0001.
Вариант 27
1. Найти действительный корень уравнения, лежащего в интервале [0.1;0.125] с точностью 10-4:
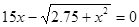
2. Решить систему линейных уравнений с точностью 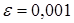
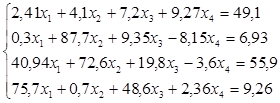 ,
,
Вариант 28
1. Отделить корни уравнения 2x4+3x3+5x2-18=0 графически и уточнить один из них методом Ньютона с точностью 0,001.
2. Составить программу, вычисляющую заданный интеграл по формуле Гусса. Составить программу-функцию для вычисления значений подъинтегральной функции. Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. Вычислить абсолютную и относительную погрешность.
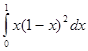
Вариант 29
1.
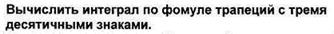
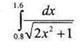
Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Вариант 30
1.

Вычислить абсолютную и относительную погрешность.
2. Для уравнения sin(x2)+cos(x2)-10x=0 на промежутке [0,10] отделить корни с шагом hx =1 графически и и уточнить один из них методом касательных с точностью до 0,001.
Задание 3
Составить схему алгоритма и написать программу
Вариант 1
Дан массив Q - [ q [ i, j], i =1,10; j=1,10]
(элементы выбираются случайным образом):
1. *Найти сумму элементов, удовлетворяющих условию 1 < q [i, j] <18.
2. Вывести на экран индексы не нулевых элементов.
3. Найти максимальный отрицательный элемент.
4. * Произведение положительных элементов главной диагонали матрицы.
i + j – 1 , если j - четно и i >3
5. Построить массив qi,j = { 
 i 2 + 1, в остальных случаях
i 2 + 1, в остальных случаях
6. Дано целое число. Вычислить произведение цифр в числе.
7. С клавиатуры вводится текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Выдать на экран преобразованный текст, удалив из него все гласные буквы.
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант2
Дан массив M - [ { м [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. * Вывести номера не нулевых элементов
2. Посчитать количество нулевых элементов.
3. Записать в этот же массив сначала все отрицательные числа и нули, затем все положительные, сохраняя порядок их следования.
4. *Найти сумму отрицательных элементов главной диагонали.
5. Найти min- элемент 1-го столбца.
6. Найти первую цифру в целом положительном числе.
7. С клавиатуры вводится текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Посчитать количество цифр в этом тексте.
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
_______________________________________________________________
Вариант3
Дан массив C = [ {C [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1.* Вывести на печать элементы, стоящие в позициях i >2 и j >4.
2. Найти минимальный элемент матрицы.
3. * Найти произведение элементов 1-ой и 4-ой строки.
4. Упорядочить массив по не возрастанию 2-ой строки.
5.Вычислить сумму элементов главной диагонали, расположенных на нечетных позициях.
6. Дано целое число. Вычислить сумму цифр в числе.
7. С клавиатуры вводится текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Выдать на экран введенный текст, удалив из него все вхождения буквы «а».
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
* - этот пункт выполнить в виде подпрограммы.
Вариант4
Дан массив A = [ { a [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. * Найти количество элементов, удовлетворяющих условию
0 < a [i, j]≤8.
2. Посчитать сумму элементов побочной диагонали.
3. *Найти максимальные элементы 3 и 5 строки.
4. Найти произведение элементов, стоящих на четных позициях.
5. Упорядочить массив по не возрастанию элементов пятого столбца.
6. Определить является ли натуральное число N СТЕПЕНЬЮ ЧИСЛА 3.
7. С клавиатуры вводится текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Какая буква встречается чаще: буква «а» или буква «о».
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант5
Дан массив К = [ {к [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. * Найти произведение элементов 2 столбца.
2. Найти положительный минимальный элемент.
3. Посчитать количество отрицательных элементов.
4. Найти max – элементы в 3 и 4 столбце и сложить их.
5. Суммировать элементы 1 и 5 строки, полученную строку сделать первой, полученную матрицу вывести на печать.
6. Дано целое число. Вычислить частное цифр в числе.
7. С клавиатуры вводится текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Выдать на экран преобразованный текст, удалив из него все согласные буквы.
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
.
Вариант6
Дан массив B = [ {b [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. Посчитать количество отрицательных элементов, стоящих на позициях с четной суммой индексов.
2. * Найти max – элемент в каждой строке.
3. Создать массив из элементов, которые > 3.
4. Найти сумму отрицательных элементов главной диагонали.
5. Упорядочить массив по не убыванию элементов 1 строки.
6. Найти вторую цифру в целом положительном числе.
7. С клавиатуры вводится текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Посчитать количество знаков препинания в этом тексте.
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
* - этот пункт выполнить в виде подпрограммы.
Вариант7
Дан массив B = [ {b [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. Посчитать сумму элементов 5 строки, стоящих на четных позициях
2. * Вывести все отрицательные элементы массива.
3. Найти min-элемент.
4. Найти произведение элементов, стоящих на местах с четной суммой индексов.
5. Найти среднюю величину положительных элементов главной диагонали.
6. Дано целое положительное число. Определите сумму цифр в числе.
7. С клавиатуры вводиться текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Выдайте на экран введенный текст, удалив из него все вхождения буквы «а».
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
* - этот пункт выполнить в виде подпрограммы.
Вариант8
Дан массив P = [ {p [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. * Найти сумму элементов 1 и 2-ой строки.
2. Вывести на экран все элементы > 5.
3. Найти max-положительный элемент главной диагонали.
4. Найти произведение элементов, стоящих на позициях с нечетной суммой индексов.
5. Упорядочить массив по не убыванию элементов 4 столбца.
6. Определить, является ли натуральное число N степенью числа 3 или нет.
7. С клавиатуры вводиться текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Какая буква в тексте встречается чаще: буква «а» или буква «о».
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение.
Вариант9
Дан массив Q = [ {q [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. * Найти количество отрицательных элементов побочной диагонали.
2. Найти сумму элементов 6 строки, стоящих в нечётных позициях.
3. Перемножить 5 и 8 строки матрицы.
4. Вывести на экран в обратном порядке элементы 2 столбца, увеличенные на 5..
5. Упорядочить массив по не убыванию элементов 9 столбца.
6. Дано целое положительное число. Вывести на экран только те цифры этого числа, которые делятся на два без остатка.
7. С клавиатуры вводиться текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Преобразуйте этот текст, заменив в нем все буквы «а» на буквы «о».
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
* - этот пункт выполнить в виде подпрограммы.
Вариант10
Дан массив A = [ {a [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. Найти наибольший элемент в 7-ой строке и поставить его первым.
2. Поменять местами 3 и 6 столбец, вывести полученную матрицу на экран.
3. Найти сумму max-элементов, каждого столбца.
4. Вычислить произведение элементов побочной диагонали <7.
5. * Посчитать количество нулевых, отрицательных и положительных элементов.
6. Определить, является ли натуральное число N степенью числа 4 или нет.
7. С клавиатуры вводиться текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Выдайте сообщение: «Слишком длинное!», если во введенном тексте больше 10 слов.
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант11
Дан массив M = [ {м [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. * Найти наибольший элемент в 1-ой строке.
2. Найти сумму элементов 2-го столбца, стоящих на местах с суммой индексов<6.
3. Сложить элементы главной и побочной диагонали.
4. Вывести на экран индексы нулевых элементов.
5. Построить новый массив М, где
i+j+1, i- четно
М [ i, j] = { i + j2, если i-нечётно и j ≤ 5
i, в остальных случаях
6. Дано целое положительное число. Найдите сумму цифр, стоящих в этом числе на четных местах.
7. С клавиатуры вводиться текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Выдайте на экран введенный текст, но удалив из него все пробелы.
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант12
Дан массив M = [ {м [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. Найти наименьший элемент в третьей строке и прибавить его ко всем элементам массива.
2. Найти произведение элементов главной диагонали.
3. * Создать массив Р = {Р1, Р2, … Рn }, где каждое значение Рi является первым элементом i-ой строки.
4. Вывести на экран элементы побочной диагонали, умноженные на 2.
5. Сложить элементы 1 и 9 строки.
6. Дано целое положительное число. Найдите произведение цифр, стоящих в этом числе на нечетных местах.
7. С клавиатуры вводиться текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Посчитайте, сколько раз в тексте встретилась буква «а».
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант13
Дан массив К = [ {к [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. Посчитать количество нулевых и положительных элементов массива.
2. * Найти сумму элементов главной диагонали.
3. Сложить элементы 5 и 7 строки.
4. Создать массив Р = {Р1, Р2, … Рn }, где каждое значение Рi является min- элементом i-ой строки.
5. Вывести на экран транспонированную матрицу.
6. Определить, является ли натуральное число N степенью числа 5 или нет.
7. С клавиатуры вводиться текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Посчитайте количество слов в тексте.
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант14
Дан массив О = [ {о [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант15
Дан массив С = [ {с [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант16
Дан массив К = [ {к [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
1. Найти количество элементов, отличных от нуля.
2. Найти max- элемент главной диагонали и вывести его индексы на экран.
3. Вычислить отношение суммы элементов 5 строки к сумме элементов 4 столбца.
4. Вычислить количество одинаковых минимальных элементов.
5. * Упорядочить 1 строку в порядке возрастания.
6. Найти первую цифру в целом положительном числе.
7. С клавиатуры вводиться текст. Слова разделяются пробелом. Ввод текста прекращается после нажатия на клавиатуре точки. Посчитайте количество цифр в этом тексте.
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант17
Дан массив M ={ [ м [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
[-10, +3 ].
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант18
Дан массив D = [ {d [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант19
Дан массив Y = [ {y [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант20
Дан массив M = [ {м [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант21
Дан массив Р = [ {р [i, j] }, i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
Если невозможно выполнить тот или иной пункт, то необходимо выдать соответствующее сообщение
Вариант22
Дан массив Q = [ q [i, j], i=1,10; j=1,10 ]
(элементы выбираются случайным образом):
Дата добавления: 2015-10-31; просмотров: 188 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| БЕЗПОСЕРЕДНІЙ ПІСЛЯОПЕРАЦІЙНИЙ ДОГЛЯД | | | Пример решения 2 |