Св-ва опред интеграла

Значение о.и. не зависит от обозначения переменной интегрирования.

Если , x € [a;b]
19.Свойства определенного интеграла: теорема об интегрировании неравенств, теоремы об оценке интеграла.

1.

2.

3.

4.

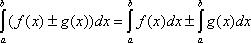
5. ,где к -постоянная.

6. Если всюду на отрезке [a, b] функция неотрицательна то ,

а если то .

7. Если на отрезке [a, b] функции и удовлетворяют условию , то ---теорема об интегрировании неравенств.

8. Если на отрезке [a, b] функция удовлетворяет условию , то определенный интеграл удовлетворяет неравенству .

9. Определенный интеграл от функции , непрерывной на отрезке [a, b], равен значению подынтегральной функции в некоторой «средней» точке с промежутка интегрирования, умноженному на длину этого промежутка:

10. Если на отрезке [a, b] функция непрерывна и Ф(х) ,то справедливо равенство Ф’(х)= , т.е. производная опр.интеграла от непрерыв.ф-ции по его переменному верхнему пределу х существует и равна значению подынтегр.функции при том же х.

Если ф-ция непрерывна на отрезке [a, b] и F(x)-какая-либо первообразная для на этом отрезке,то справедлива формула Ньютона-Лейбница:

Теорема о среднем. Ее геометрическая и экономическая интерпретация.

Теорема о среднем

Первая теорема о среднем

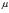( - среднее значение функции).

Если f непрерывна, то

Вторая теорема о среднем

Если f, g непрерывны, а g не меняет знак, то

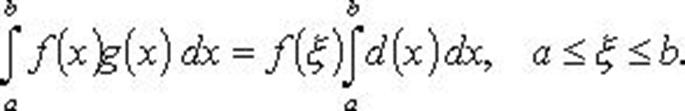
Формула Бонне

(g монотонна).

Теорема об интеграле с переменным верхним пределом. (дополнительный вопрос)

Произв-я опр. инт-ла от непрерывн. ф-ии по верхнему пределу = знач. подинт. ф-ии.
22.Формула Ньютона-Лейбница.

Для неопр. ф-ии y=f(x) на конечн. отр-ке, опред. инт-л нах-ся как первообр-ая ф-ии f(x) в пред-х от а до b. Ф-ла справедлива при усл-х: y=f(x) непрерывна на (а,в), (а,в) должен быть конечным.

Если ф-ция непрерывна на отрезке [a, b] и F(x)-какая-либо первообразная для на этом отрезке,то справедлива формула Ньютона-Лейбница:

Дата добавления: 2015-10-31