Геометрическая интерпретация общего решения и решения задачи Коши.

Геометрический смысл задачи Коши состоит в определении той интегральной кривой, которая проходит через заданную точку

Однопараметрическое семейство функций 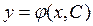, зависящих от параметра С из некоторой области и непрерывно дифференцируемых по х в некотором интервале (a,b), называется общим решением уравнения

, где f – заданная функция двух переменных, определенная в некоторой области , если:

1. Функция 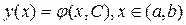, является решением данного уравнения для любого фиксированного С и из области .

2. Для любых начальных условий 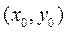из области D существует 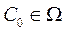такое, что .

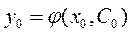Линейные дифференциальные уравнения I порядка и уравнения Бернулли.

Имеют вид: y’=f(x,y) (1) F(x,y,y’)=0 (2)

1) y’=f(x) dy/dx=f(x)

dy=f(x)dx òdy=òf(x)dx y=òf(x)dx

2) y’=f(y) dy/dx=f(y)

25.

3) f(x)dx=f(y)dy ДУ с разделенными переменными òf(x)dx=òf(y)dy

4)y’=f(x)gy или M(x)N(y)d(x)=K(x)L(y)d(y)

ДУ с разделяющимися переменными

Ур-е вида (4) реш по схеме:

d(y)/d(x)=f(x)gy

d(y)/g(x)=f(x)d(x)

M(x)d(x)/K(x)=L(y)d(y)/N(y)

26.

5) y’=g(y/x) однородное ДУ 1го порядка(ф-ция вида f(αx,αy)=α^kg(x,y) наз однор ф-ция k-того порядка,αЄR)

реш с помощью подстановки

z=y/x y=zx y’=z’_xx+z

z’x+z=g(z) d(z)/(g(z)-z)=d(x)/x

6) y’=f(ax+by) приводится к ур-ю вида (4) путем замены z=ax+by

Структура общего решения линейного однородного дифференциального уравнения II порядка.

Обыкн ДУ 2 порядка с пост.коэфф. имеет вид:

(1) y``+py`+qy=r(x) p,q принадл. R, r(x) – функция

Если r(x) =0, то

(2) y``+ py`+qy=0 – однор.лин.ДУ с пост.коэфф.

Ур-е вида (3) 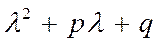=0 – характерист.ур-е (1) и(2) Стр-ра общего решения ур.(2) определяется корнями квадр.ур-я. (3)

Возможны 3 случая

1. кв.ур-е имеет разные корни α1 α2, D>0 тогда общее решение:

y=C1 C1, C2 прин.R

2. корни кв.ур. кратные, т.е. α1= α2=α; D=0

y= C1, C2 прин.R

3. корни комплексно сопряженные: λ1= α-βi; λ2= α+βi;

y= C1 C1, C2 прин.R

Метод Эйлера нахождения общего решения ОЛДУ II с постоянными коэффициентами.

Линейное дифференциальное уравнение второго порядка вида: называется дифференциальным уравнением Эйлера.

Простейший одношаговый метод численного решения задачи Коши — метод Эйлера. В методе Эйлера величины вычисляются по формуле: :

y' = f(x, y), y(a) = , x ∈ [a, b],

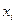= a + ih, h = (b-a)/N, i = 0,1, 2,..., N,

y()≈ ,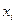

.

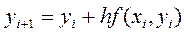Дата добавления: 2015-10-31