Понятие несобственных интегралов I рода. Пример интеграл Дирихле I рода.

НИ1 -это опр инт-л от непереывн ф-ии на бесконеч отр-ке интегрир-я. Бескон отр инт-я может быть 3-ёх видов 1. 2. 3. . По опред-ю НИ1 это предел от опред инт-ла . На 1-ом этапе вычисл опр инт от а до в по ф-ле Н-Л, на 2-ом предел получ-ой ф-ии зависящей от b, т.к. это этап вычисл-я пред-ла, то от его реализ-ии зависит ответ. Если получено число, то НИ1 сходится к этому числу; если то расх-ся.

Понятие несобственных интегралов II рода. Пример интеграл Дирихле II рода.

НИ2 -это опр инт-л от ф-ии, имеющей разрыв 2-го рода на конечн отр-ке инт-ия. Если т-ка разрыва 2-го рода совпала с левым концом инт-ия, то . Если т-ка раз-ва 2-го рода совпала с левой границей инт-ия(т. b), то 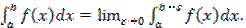если т. разрыва попала в к-ую-либо точку с, то

Понятие дифференциального уравнения I порядка, его общего и частного решения.

Ур-е вида f(x,y,y`)=0 наз-ют обыкновенным ДУ1. Общ реш ДУ1 наз-ся ф-ия , к-я зависит от одного произвол. постоянного С и удовлетв условиям: а)она удовл-т ДУ при любом конкр. знач. С. б) каково бы ни было нач усл-е y=Yo при x=Xo, можно найти такое знач с=Со, что ф-я y= удовл-ет данному нач усл-ю. частным реш наз-ся любая ф-ия y= , к-я получ-ся из общ реш-я y= , если в последнем произвол-му постоян-му С придать опред. знач с=Со.

ДУ с разделяющимися переменными. Пример.

Уравнение вида: , а также вида: называются уравнениями с разделяющимися переменными.

Общие решения:

Пример:

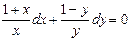
Геометрическая интерпретация общего решения и решения задачи Коши.

Геометрический смысл задачи Коши состоит в определении той интегральной кривой, которая проходит через заданную точку

Однопараметрическое семейство функций , зависящих от параметра С из некоторой области и непрерывно дифференцируемых по х в некотором интервале (a,b), называется общим решением уравнения

, где f – заданная функция двух переменных, определенная в некоторой области , если:

1. Функция , является решением данного уравнения для любого фиксированного С и из области .

2. Для любых начальных условий из области D существует такое, что .

Дата добавления: 2015-10-31