
Читайте также:
|
Для сходимости знакоположительного числового ряда  необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена. Первый признак сравнения рядов. Пусть
необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена. Первый признак сравнения рядов. Пусть  и
и 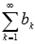 - два знакоположительных числовых ряда и выполняется неравенство
- два знакоположительных числовых ряда и выполняется неравенство  для всех k =1, 2, 3,... Тогда из сходимости ряда
для всех k =1, 2, 3,... Тогда из сходимости ряда 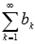 следует сходимость
следует сходимость 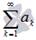 , а из расходимости ряда
, а из расходимости ряда  следует расходимость
следует расходимость  Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя k-ого члена исследуемого числового ряда. К примеру, пусть
Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя k-ого члена исследуемого числового ряда. К примеру, пусть  разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с k-ым членом
разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с k-ым членом  то есть, гармонический ряд. Рассмотрим несколько примеров. Второй признак сравнения. Пусть
то есть, гармонический ряд. Рассмотрим несколько примеров. Второй признак сравнения. Пусть 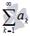 и
и  знакоположительные числовые ряды. Если
знакоположительные числовые ряды. Если  то из сходимости ряда
то из сходимости ряда 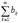 следует сходимость
следует сходимость  Если
Если  то из расходимости числового ряда
то из расходимости числового ряда  следует расходимость
следует расходимость 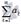 Следствие. Если
Следствие. Если  и
и  то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость. Третий признак сравнения. Пусть
то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость. Третий признак сравнения. Пусть 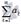 и
и  знакоположительные числовые ряды. Если с некоторого номера N выполняется условие
знакоположительные числовые ряды. Если с некоторого номера N выполняется условие 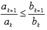 то из сходимости ряда
то из сходимости ряда 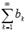 следует сходимость
следует сходимость  а из расходимости ряда
а из расходимости ряда 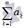 следует расходимость
следует расходимость 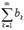 Признак Даламбера. Пусть
Признак Даламбера. Пусть 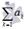 - знакоположительный числовой ряд. Если
- знакоположительный числовой ряд. Если 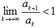 то числовой ряд сходится, если
то числовой ряд сходится, если  то ряд расходится. Замечание. Признак Даламбера справедлив, если предел бесконечен, то есть, если
то ряд расходится. Замечание. Признак Даламбера справедлив, если предел бесконечен, то есть, если  , то ряд сходится, если,
, то ряд сходится, если,  то ряд расходится. Если
то ряд расходится. Если 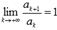 , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование. Радикальный признак Коши. Пусть
, то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование. Радикальный признак Коши. Пусть  - знакоположительный числовой ряд. Если
- знакоположительный числовой ряд. Если  , то числовой ряд сходится, если
, то числовой ряд сходится, если 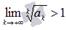 , то ряд расходится. Замечание. Радикальный признак Коши справедлив, если предел бесконечен, то есть, если
, то ряд расходится. Замечание. Радикальный признак Коши справедлив, если предел бесконечен, то есть, если 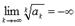 , то ряд сходится, если
, то ряд сходится, если  , то ряд расходится. Если
, то ряд расходится. Если  , то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование. Обычно достаточно легко разглядеть случаи, когда лучше всего использовать радикальный признак Коши. Характерным является случай, когда общий член числового ряда представляет собой показательно степенное выражение. Рассмотрим несколько примеров. Интегральный признак Коши. Пусть
, то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование. Обычно достаточно легко разглядеть случаи, когда лучше всего использовать радикальный признак Коши. Характерным является случай, когда общий член числового ряда представляет собой показательно степенное выражение. Рассмотрим несколько примеров. Интегральный признак Коши. Пусть  - знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции
- знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции 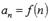 . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале
. Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале  , где
, где  ). Тогда в случае сходимости несобственного интеграла
). Тогда в случае сходимости несобственного интеграла  сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.При проверке убывания функции y = f(x) на интервале
сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.При проверке убывания функции y = f(x) на интервале 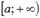 Вам может пригодится теория из раздела возрастание и убывание функции.
Вам может пригодится теория из раздела возрастание и убывание функции.
Дата добавления: 2015-10-31; просмотров: 207 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Понятие несобственных интегралов I рода. Пример интеграл Дирихле I рода. | | | Интегрирование простейших дробей |