Відмінності стандартної та канонічної форми запису задач лінійного програмування

Визначення економіко-математичної моделі

· Під економіко-математичною моделлю розуміють концентроване вираження найсуттєвіших економічних процесів у вигляді функцій, рівнянь та нерівностей.

· Це опис кількісних взаємозв*язків та взаємозалежностей економічних систем чи процесів в економічній формі.

· Економіко - математична модель – це математична модель економічної системи, явища, процесу

· Еконо́міко-математи́чні моде́лі — моделі економічних об'єктів або процесів, при описі яких використовуються математичні засоби.

· Моделлю деякої системи називають штучну систему або об'єкт, що в певних умовах може замінити систему-оригінал (об'єкт) шляхом відтворення властивостей і характеристик оригіналу, які цікавлять дослідника, коли така заміна дає істотні переваги у зручності дослідження.

· Економ-Математична модель — це абстракція реальної економічної дійсності, в якій відношення між реальними елементами, що ці­кавлять дослідника, замінені відношеннями між математичними категоріями.

2. Визначення ризику Ризик – це а) такі умови моделювання, при яких статистичні особливості явищ, здатних змінити вхідні параметри математичної моделі, не є певними, але ймовірність кожного результату відома;

Відмінності стандартної та канонічної форми запису задач лінійного програмування

; .

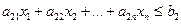
Канонічна форма запису відрізняється від стандартної тим, що в обмеженнях задачі замість системи нерівностей має місце система рівнянь, яка простими математичними діями типу доповнення лівої частини додатковими змінними отримана з нерівностей (2.2)

........................................................ (2.3)

; .

4. Порядок отримання цілочислового розв’язку з нецілочисливого задачі лінійного програмування…………………….. 1) симплексним методом розв’язуємо задачу ЛП, яка відповідає не цілочисловому розв’язку; 2) до останньої ітерації добавляють ще одне обмеження. Це обмеження має відповідати умові, щоб всі допустимі цілочислові точки відповідали йому, а оптимальна точка нецілочислового розв'язку – ні. 3) для занесення в симплексну таблицю перетворюємо цю нерівність у рівняння,ввівши додаткову змінну; 4)отримане рівняння множимо на (-1) і заносимо в таблицю як Fопт. 5) розв’язуємо симплексним методом, поки у рядку Fопт не будуть цілі числа.

5. Які розділи математики використовуються в економіко-математичному моделюванні……………………….. математичної статистики, теорії імовірностей, математичного програмування, лінійної алгебри, систем нелінійних рівнянь та ін.

Дата добавления: 2015-10-31