
|
Читайте также: |
Уверен [ Действие(b) не есть «принять и выполнить»(x)],
Предполагает [ Действие(b) есть «принять и выполнить»(x)],
Сомневается [ Действие(b) есть «принять и выполнить»(x)],
Уверен [ Действие(b) есть «принять и не выполнить»(x)],
Уверен [ Действие(b) не есть «принять и не выполнить»(x)],
Предполагает [ Действие(b) есть «принять и не выполнить»(x)],
Сомневается [ Действие(b) есть «принять и не выполнить»(x)],
Уверен [ Действие(b) есть «не принять и выполнить»(x)],
Уверен [ Действие(b) не есть «не принять и выполнить»(x)],
Предполагает [ Действие(b) есть «не принять и выполнить»(x)],
Сомневается [ Действие(b) есть «не принять и выполнить»(x)],
Уверен [ Действие(b) есть «принять и не выполнить»(x)],
Уверен [ Действие(b) не есть «не принять и не выполнить»(x)],
Предполагает [ Действие(b) есть «не принять и не выполнить»(x)],
Сомневается [ Действие(b) есть «не принять и не выполнить»(x)],
}
Пусть теперь эндоагент – это торговая фирма, а экзоагент – клиент этой фирмы. Этому случаю соответствует режим коммуникации C2B (client to business). Здесь переговоры начинает клиент, причём его запросы можно классифицировать на четыре группы.
К первой группе относятся чётко направленные запросы. Назовем их «корректными». Это запросы вида Уверен(X есть «желаемое», Y есть «желаемое»), т.е. М(X ecть E), где M – степень уверенности, X – класс запрашиваемых продуктов, E – экземпляр данного класса.
Ко второй группе относятся «недоопределёные» запросы, т.е. высказывания вида Предполагаю(X есть «желаемое», Y есть «желаемое»). Здесь клиент не уверен в том, что он хочет, но знает что ему определенно что-то нужно.
В третью группу отнесём «противоречивые» запросы, т.е. высказывания вида Сомневаюсь(X есть «желаемое»,Y есть «желаемое»). От клиента поступает противоречивая информация о том, что он хочет, клиент не способен сформулировать релевантный запрос.
В четвёртой группе останутся заведомо «некорректные» запросы вида: Уверен(X не есть «желаемое», Y не есть «желаемое»). Клиент попал не по адресу или намеренно вводит фирму в заблуждение относительно своих намерений.
Ответы фирмы также можно классифицировать как «релевантные», «нерелевантные», «контрпредложения», и «отказы». Например, «Релевантные» = Уверен (X есть «то, что Вам надо», Y есть «то, что Вам надо»), «Отказ» = Уверен (X не есть «то, что Вам надо», Y не есть «то, что Вам надо»), «Контрпредложение» = Предполагаю (X есть «то, что Вам надо», Y есть «то, что Вам надо»), «Нерелевантный» = Сомневаюсь (X есть «то, что Вам надо», Y есть «то, что Вам надо»).
В приведённых терминах можно построить вопросно-ответную систему, каждый вариант диалога которой описывается парой значений. Например («корректный», «релевантный») или («корректный», «отказ») или («амбивалентный», «контрпредложение»). Очевидно, что всего возможно шестнадцать пар значений.
Для работы со знаниями в подобных случаях рефлексии построим LREF16 – шестнадцатизначную немонотонную логику на базе декартова произведения логик экзо и эндоагентов. Эта логика имеет в качестве истинностных значений пары, составленные из истинностных значений базовых логик [86]. При этом будем называть первый компонент пары значений внутренним значением, а второй компонент – внешним.
Введем следующие обозначения: эндоагент – а, экзоагент – b. Для внешнего значения X и внутреннего значения Y, соответствующих логическому значению v = <X,y> логики LREF16, которое приписано некоторой формуле Z, варианты интерпретация приведены в табл.1.
Определим на множестве значений построенной решётки логики LREF16 отношения частичного порядка. Для этого введем сначала отношения порядка на множествах Vint ={T, F, N, A} и Vext ={t, f, n, a}.
Таблица.3.17 Интерпретация истинностных значений <X,y> логики LREF16, если эндоагент есть a, а экзоагент – b
| Значение | Интерпретация |
| <T, t> | «a уверен в том, что b уверен в Z» |
| <T, f> | «a уверен в том, что b уверен что не Z» |
| <T, n> | «a уверен в том, что b ничего не знает о Z» |
| <T, a> | «a уверен в том, что b считает Z противоречивым» |
| <F, t> | «a уверен, что неправда, что b уверен в Z» |
| <F, f> | «a уверен, что неправда, что b уверен что не Z» |
| <F, n> | «a уверен что неправда, что b ничего не знает о Z» |
| <F, a> | «a уверен что неправда, что b считает Z противоречивым» |
| <N, t> | «a ничего не знает о том, что b уверен в Z» |
| <N, f> | «a ничего не знает о том, что b уверен, что не Z» |
| <N, n> | «a ничего не знает о том, что b ничего не знает о Z» |
| <N, a> | «a ничего не знает о том, что b считает Z противоречивым» |
| <A, t> | «a считает противоречивым то, что b уверен в Z» |
| <A, f> | «a считает противоречивым то, что b уверен, что не Z» |
| <A, n> | «a считает противоречивым то, что b ничего не знает о Z» |
| <A, a> | «a считает противоречивым то, что b считает Z противоречивым» |
Пусть £intT – отношение внутренней истинности:
v1 £ intT v2 Û (v1 = v2) или (v2 = T) или (v1 = F), где v1,v2 Î Vint
Пусть £extT – отношение внешней истинности:
v1 £ extT v2 Û (v1 = v2) или (v2 = t) или (v1 = f), где v1,v2 Î Vext
Пусть £extI – отношение внутренней информативности:
v1 £ intI v2 Û (v1 = v2) или (v2 = A) или (v1 = N), где v1,v2 Î Vint
Пусть £extI – отношение внешней информативности:
v1 £ extI v2 Û (v1 = v2) или (v2 = a) или (v1 = n), где v1,v2 Î Vext
| A,a |
| N,n |
| T,t |
| F,f |
| F,a |
| A,f |
| F,n |
| N,f |
| A,t |
| T,a |
| T,n |
| N,t |
| A,n |
| N,a |
| T,f |
| F,t |
| (a) |
| T,t |
| F,f |
| A,a |
| N,n |
| N,t |
| T,n |
| N,f |
| F,n |
| T,a |
| A,t |
| A,f |
| F,a |
| T,f |
| F,t |
| A,n |
| N,a |
| (b) |
| T,a |
| F,n |
| A,t |
| N,f |
| N,a |
| T,f |
| N,n |
| F,f |
| T,t |
| A,a |
| A,n |
| F,t |
| T,n |
| F,a |
| A,f |
| N,t |
| (c) |
| A,t |
| N,f |
| T,a |
| F,n |
| F,t |
| A,n |
| F,f |
| N,n |
| A,a |
| T,t |
| T,f |
| N,a |
| A,f |
| N,t |
| T,n |
| F,a |
| (d) |
Рис. 3.14 Решётка логики LREF16 в отношении истинности (a), информативности (b), внешнего порядка (c) и внутреннего порядка (d).
На базе всех четырёх порядков можно построить операции «и» и «или» как операции взятия верхней и нижней грани [115,116,176]. Но логические операции будем строить только на базе двух последних отношений.
Множество L логических связок разделим на три подмножества: L = Lint È Lext È Lcomb, где Lint – множество внутренних (эндогенных) логических связок, Lext – множество внешних (экзогенных) логических связок, Lcomb – множество комбинированных логических связок. Комбинированные операции являются специальными операциями по изменению статуса знаний (их переводу из внешних во внутренние и наоборот). Имеем Lint = {Ø, ‘, Ù, Ú} – для вывода на внутренних знаниях;
Lext = {~, “,&, | }– для вывода на внешних знаниях; Lcomb={*} – для изменения статуса знаний.
Пусть j – функция приписывания значений пропозициональным переменным. Тогда jA будет означать результат приписывания значений всем пропозициональным переменным в формуле A.
Пусть |jA| означает «значение формулы A при приписывании j». |jA| Î V. Теперь можно задать правила приписывания значений сложным формулам.
Внутреннее отрицание Ø:
|jØA| = <not(X),y> Û |jA| = <X,y>,
not(X)=T еcли X=F, not(X)=F если X=T и not(X)=X если XÎ{A,N}.
Внешнее отрицание ~:
|j ~A| = <X,not(y)> Û |jA| = <X,y>,
not(y) = t еcли y=f, not(y)=f если y=t и not(y)=y если yÎ{a,n}.
Для внутренней инверсии определенности ‘:
|j‘A| = <inv(X),y> Û |jA| = <X,y>,
inv(X)=A еcли X=N, inv(X)=N если X=A и not(X)=X если XÎ{T,F}.
Для внешней инверсии определённости “:
|j“A| = <X,inv(y)> Û |jA| = <X,y>,
inv(y)=a еcли y=n, inv(y)=n если y=A и not(y)=y если yÎ{t,f}.
Для внутреннего «и» Ù:
|jAÙB| = v Û |jA| = va, |jB| = vb и v наименьшая верхняя грань va и vb для решетки в отношении £int
Для внешнего «и» &:
|jA&B| = v Û |jA| = va, |jB| = vb и v наименьшая верхняя грань va и vb для решетки в отношении £ext
Для внутреннего «или»:
|jAÚB| = v Û |jA| = va, |jB| = vb и v наименьшая нижняя грань va и vb для решетки в отношении £int
Для внешнего «или» |:
|jA|B| = v Û |jA| = va, |jB| = vb и v наименьшая верхняя грань va и vb для решетки в отношении £ext
Для операции рефлексивного перехода *:
|j^A| = <X,y> Û |jA| = <T,x>, x» X.
Здесь x» X означает, что x и X это аналогичные значения в своих проекциях, т.е. x» X Û (x = t и X = T) или (x = f и X = F) или (x = a и X = A) или (x = n и X = N).
Построенное множество логических операций и их интерпретация позволяют осуществлять логический вывод на множестве истинностных значений логики LREF16 и, в конечном итоге, работать с рефлексивными знаниями на уровне исчисления рефлексивных высказываний.
Выводы по третьей главе.
Следующие основные результаты, были получены в третьей главе:
· Предложен новый подход к моделированию диалога на основе многозначных логик.
· Сформулированы основные принципы построения диалоговых логик и их отличия от логик, традиционно использующихся для моделирования диалога.
· Рассмотрены различные варианты диалоговых логик: простейшая четырёхзначная, шести- и восьми- значные, а также модализированные и нечёткие логики диалога.
· Для базовой четырёхзначной логики разработан механизм вывода на базе аналитических таблиц.
· Дано формальное описание построения диалоговых логик как диалогового произведения базовых логик агентов участников, доказана функциональная полнота операций на диалоговом произведении логик.
· Построен механизм вывода на диалоговом произведении и доказана его состоятельность.
· Предложен подход к моделированию рефлексивных рассуждений (внутреннего диалога) и пополнения знаний агента на основе многозначных диалоговых логик.
В главе 4 будут разработаны методы и алгоритмы автоматизированного использования диалоговых логик, а также даны примеры применения их при построении RM-систем.
4. ПРОГРАММНЫЕ АГЕНТЫ ПОДДЕРЖКИ УПРАВЛЕНИЯ ВЗАИМОДЕЙСТВИЕМ С ПОСТАВЩИКАМИ И ЗАКАЗЧИКАМИ
В предыдущей главе были проанализированы существующие, а также построены авторские модели и средства описания диалогов в агентно-ориентированных системах. Главная задача этой главы – описать методы и алгоритмы, при помощи которых возможно построение интеллектуальных многоагентых систем поддержки управления взаимодействием с поставщиками и заказчиками.
4.1 Компьютерное моделирование диалога агентов на базе диалоговых логик
Практическое использование диалоговых логик требует соответствующей алгоритмической базы, в которую должны быть включены следующие элементы:
· алгоритмы представления диалоговых данных, знаний и целей агентов на языке диалоговой логики;
· алгоритмы диалогового вывода;
· алгоритмы координации, принятия решений и их последующей реализации.
Каждый элемент заслуживает развернутого рассмотрения.
4.1.1 Представление знаний, мнений и целей агентов на языке диалоговой логики.
Допустим, существует некоторое высказывание Х. Это высказывание может представлять собой убеждение или знание агента A. Согласно [19], знанием является обоснованное истинное мнение (убеждение). Однако, в рамках данной работы, мы не будем исследовать процесс обоснования и подтверждения тех или иных знаний, нас будет интересовать лишь мнение М агента А относительно утверждения Х. Пусть запись M(A)[X] – означает агент А имеет относительно утверждения Х мнение M.
В случае диалога имеем набор агентов A1,A2,…,AN, приведённая выше запись примет вид: <M1,M2,…,Mn>(<A1,A2,…,An>)[X]. Если набор агентов не меняется в процессе диалога, то его можно опустить. Необходимо заметить, что в любом конечном диалоге можно выбрать такое минимальное множество агентов, которое будет включать всех агентов, участвующих в диалоге. Итак, исходная запись примет вид <M1,M2,…,Mn>[X]. Опять-таки, в силу конечности диалога, набор мнений каждого конкретного агента ограничен. Поставим в соответствие этому набору мнений логику агента, тогда диалоговое произведение логик агентов участников образует логику диалога, а любой набор <M1,M2,…,Mn> будет её значением. Таким образом, мы можем перейти к простой записи в стиле утверждения высказываний X = М. Причем Х может быть фактом, а может быть высказыванием любого произвольного вида, включающем любые виды логических связок.
Описанным образом можно определить значения всех утверждений, встречающихся в процессе диалога. Аналогичным образом задаются цели и правила диалога.
Рассмотрим пример диалога клиента с поставщиком. Предположим, p1,p2,p3,p4 – доставка товара 1, 2, 3 и 4 соответственно, а m и n – дополнительные условия доставки, допустим m-«поставка пойдет по увеличенной цене», n-«срок поставки увеличивается». Пусть, агент-поставщик может поставить товары 1 и 3, доставка товара 2 может затянуться, а товар 4 идет по новой цене, тогда его база знаний будет выглядеть так (рассмотрим простую бинарную логику):
p1®T, p2®n, p3®T, p4®m,
или же просто: p2®n, p4®m.
Клиент желает заказать товар 1 и 2. Также, он может использовать совокупность товаров 3 и 4 как замену товару 2. Кроме того, он согласен заплатить большую цену, но не хочет ждать. Его база знаний выглядит так:
p1 Ù s2, s2®(p3Ùp4)Úp2, , Øn, m
Перейдём к логике диалога:
< (&p2®&nn) Ù (&p4®&m),
(p1 Ù s2) Ù (s2®(p3Ù&p4)Ú& p2) Ù (&nØn) Ù &m> (4.1)
Как видим, знания агентов остаются без изменений, но во все литеры требующие взаимодействия добавляется индексированная операция смешивания. Это необходимо для того, чтобы синхронизировать литеры требующие взаимодействия. Поясним на примере, пусть известно, что заказчику нужен товар А или Б, и поставщик может доставить товар А или Б. Возможны следующие интерпретации, удовлетворяющие обоим условиям: А=<F,T>,Б=<T,F>;А=<T,F>,Б=<F,T>. Однако в обоих случаях сделка между поставщиком и заказчиком не достижима. Очевидно, использование операции смешивания в качестве обозначения взаимодействия снимает такие проблемы.
Возвращаясь к исходному примеру, если сделка между поставщиком и заказчиком возможна, то формула (4.1) будет выполнима, более того, каждая истинностная интерпретация будет означать один из вариантов достижения соглашения.
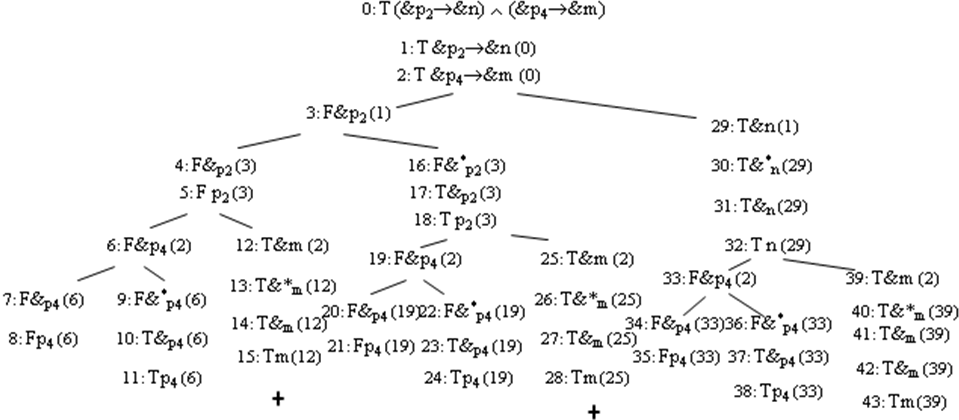
Построим деревья вывода для обеих частей приведённой формулы (см. рис 4.1):
 (а)
(а)
 (b)
(b)
Рис 4.1. Деревья вывода для примера диалога клиента и поставщика, «+» обозначены сопрягаемые ветви.
На рис 4.1 «+» обозначены взаимно сопрягаемые ветви деревьев вывода. Любое их сочетание дает вариант достижения соглашения, все эти варианты перечислены в следующей таблице.
Таблица 4.1 Варианты достижения соглашения для диалога клиента и поставщика
| Вариант | Поставщик | Заказчик |
| Tm Fp2 T&*m | Тp1 Тs2 Тp3 Tp4 Тm Fn T&*4 T&*m | |
| Tm Тp2 T&*m F&*2 | Тp1 Тs2 Тp3 Tp4 Тm Fn T&*4 T&*m |
Указанные в таблице варианты соглашения не полны, и необходимо достроить их, опираясь на данные, полученные в результате декомпозиции деревьев вывода. Для этого необходимо учитывать требования сопряженной ветви. В обе ветви допишем конкретизирующие означивания, в согласии с вариантом интерпретации &* сопряженных ветвей.
Таблица 4.2 Варианты достижения соглашения для диалога клиента и поставщика с учётом интерпретации &* сопряженных ветвей.
| Вариант | Поставщик | Заказчик |
| Tm Fp2 Tp4 | Тp1 Тs2 Тp3 Tp4 Тm Fn | |
| Tm Тp2 Tp4 | Тp1 Тs2 Тp3 Tp4 Тm Fn Fp2 |
Каждой их строк таблицы 4.2 соответствует набор значений исходных переменных, совокупность этих наборов представляет собой вариант решения или соглашение. Над полученным множеством соглашений, образуемых приведёнными выше вариантами сопряжения, можно производить многокритериальный поиск оптимального решения, например, классическими методами линейного программирования [8,75]. Подробнее этот способ будет описан ниже.
Диалоговая логика может применяться не только для решения задач, включающих диалог между агентами, она также может применяться в случае верификации знаний при использовании диалоговой семантики в качестве семантической базы. В этом случае мы используем единую базу знаний агента, но используем диалоговые операции для анализа высказываний с позиций взаимодействия.
Рассмотрим пример. Пусть дано &(AÙB)®&(AÚB). Высказывание читается как «из того, что по А и B найдено соглашение, следует то, что найдено соглашение по A или B». Смысл такого высказывания заметно отличен от смысла высказывания AÙB®AÚB. На рис 4.2 представлены деревья вывода формулы.


Рис 4.2. Деревья вывода формулы &(AÙB)®&(AÚB).
Ветви а1 и б1 не сопрягаются ни с самими собой, ни друг с другом, ни с одной из ветвей а2, б2, в2, г2 или д2. Это означает, что формула &(AÙB)®&(AÚB) не может принимать ни одно из значений (F,F) (T,F) или (F,T), т.е. она является тавтологией.
Рассмотрим еще один пример. Пусть дано &(A®B)®(&A®&B). Высказывание читается как «из того, что найдено соглашение о том, что из A следует B, следует то, что из соглашения по A следует соглашение по B». На рис 4.3 представлены деревья вывода формулы.


Рис 4.3. Дерево вывода формулы &(A®B)®(&A®&B).
Ветвь а1 не является самосопряженной, и не сопрягается ни с одной из ветвей а2, б2, в2, г2, д2 или е2. Это означает, что формула &(A®B)®(&A®&B) не может принимать ни одно из значений (F,F) (T,F) или (F,T), т.е. она является тавтологией.
Таким образом, диалоговая логика, в отличие от традиционной, позволяет интуитивно ясным образом работать с различными вариантами соглашений, искать оптимальные решения ситуаций, включающих взаимодействие и кооперацию.
4.1.2 Алгоритмы автоматического решения задач с использованием диалоговой логики.
Описание, приведённое ранее, достаточно для ручного анализа с использованием диалоговых логик, однако этот аппарат, также может быть применён автоматизировано. В силу специфики задач, решаемых при помощи ИИ и ИС, разработку механизмов и алгоритмов автоматического использования диалоговых логик можно считать приоритетным направлением дальнейшего исследования.
Опишем основные шаги при решении задач с помощью диалоговой логики.
1. Выбор аппроксимации и формализация мнений агентов с учётом требований и ограничений концептуальной спецификации.
2. Диалогизация мнений агента(ов) и объединение их в единой базе знаний диалога. Формулировка целей диалога.
3. Построение дерева логического вывода для выбранных формул.
4. Поиск сопряженных ветвей и сохранение результирующего множества допустимых интерпретаций.
5. Постановка и решение задачи поиска оптимального соглашения.
6. Анализ результатов и принятие решений на основании полученных данных.
Пункт 1 является нетривиальной задачей, автоматизация которой представляется достаточно затруднительной. Основные подходы к её решению будут изложены в параграфе 4.2 данной диссертации. Пункт 2 достаточно подробно был описан в предыдущем параграфе этой работы и не нуждается в дополнительном рассмотрении. Рассмотрим алгоритм построения дерева логического вывода из пункта 3 (см. рис 4.4).
Приведённый алгоритм достаточно тривиален. Его вычислительная сложность оценивается O(m*n*exp(n)), где n – количество связок формулы, m-количество агентов. В некоторых случаях, улучшить скорость работы этого алгоритма можно за счет введения эвристик, определяющих порядок применения табличных правил. Приоритетное применение правил с наименьшим ветвлением, – наиболее очевидная из таких эвристик.
В случае параллельного выполнения прослеживается естественный пространственный параллелизм, благодаря которому без каких-либо трудностей можно распределить вычисления деревьев отдельных агентов по разным узлам. Также, каждая ветвь дерева может рассчитываться в отдельном потоке. В идеальном случае, при неограниченных ресурсах распараллеливания, возможно сокращение временной сложности алгоритма до O(n).
Рис 4.4. Алгоритм построения дерева логического вывода формулы диалоговой логики с использованием аналитических таблиц.
Дата добавления: 2015-09-04; просмотров: 33 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство. 3 страница | | | Доказательство. 5 страница |