Доказательство. 1 страница

Докажем по индукции. Из леммы 3.2 следует, что для любой нульарной операции теорема выполняется.

Пусть, теорема выполняется для n-арных операций, докажем, что она тогда выполняется для (n+1)-арных операций.

Рассмотрим произвольную функцию Ф(x₁,x₂,…x_n,x_n+1). Согласно индуктивному допущению Ф(x₁,x₂,…x_n,T), Ф(x₁,x₂,…x_n,I), Ф(x₁,x₂,…x_n,E), Ф(x₁,x₂,…x_n,F) выразимы при помощи композиции операций из { ₂, é₄, Ú₁ }. Обозначим эти выражения Ф₁, Ф₂, Ф₃ и Ф₄ соответственно.

Сконструируем

Ф_new = [Ф₁ Ù₁ j₁(х_n+1)] Ú₁ [Ф₂ Ù₁ j₂(х_n+1)] Ú₁ [Ф₃ Ù₁ j₃(х_n+1)] Ú₁ [Ф₄ Ù₁ j₄(х_n+1)]

Воспользовавшись соотношениями (3.4), (3.5), (3.6) и (3.13) получим:

Ф_new= é₄₂é₄₂ [ é₄₂é₄₂ Ф₁ Ú₁ é₄₂é₄₂ j₁(х_n+1) ] Ú₁

é₄₂é₄₂ [ é₄₂é₄₂ Ф₂ Ú₁ é₄₂é₄₂ j₂(х_n+1) ] Ú₁

é₄₂é₄₂ [ é₄₂é₄₂ Ф₃ Ú₁ é₄₂é₄₂ j₃(х_n+1) ] Ú₁

é₄₂é₄₂ [ é₄₂é₄₂ Ф₄ Ú₁ é₄₂é₄₂ j₄(х_n+1) ] (3.17)

Выражение Ф_new принимает значение Ф₁, если х_n+1 = T, F₂, если х_n+1 = I, Ф₃, если х_n+1 = E и Ф₄, если х_n+1 = F, иными словами Ф(x₁,x₂,…x_n,x_n+1) = Ф_new. При любых значениях х_n+1. Теорема доказана.

Лемма 3.3 Все операции системы { ₂, é₄, Ú₁ }независимы друг от друга (не выражаются композицией остальных).

Доказательство. Очевидно, что бинарная операция Ú₁ не может быть представлена композицией унарных операций ₂ и é₄.

Операция ₃ не может быть представлена композицией ₂ и Ú₁. Рассмотрим все возможные представления:

x ¹ é₄ x

₂ x ¹ é₄ x

₂ (x Ú₁₂ x)=x Ú₁₂ x ¹ é₄ x

Все остальные представления сводимы к перечисленным трём в силу (3.4), (3.10) и (3.11).

Аналогично, операция ₂ не может быть представлена композицией é₄ и Ú₁:

x ¹ ₂ x

é₄ x ¹ ₂ x

é₄ (x Ú₁₃ x) = x Ú₁é₄ x ¹ ₂ x

Все остальные представления сводимы к этим трём в силу тех же (3.4), (3.10) и (3.11).

Лемма доказана.

Следствие 3.1. Система операций { ₂, é₄, Ú₁ } образует базис операций L_dmin.

Рассмотрим теперь различные определения операции импликации. Импликацию можно задать, как при помощи комбинации отрицания и дизъюнкции, так и независимо. Для начала рассмотрим комбинационные определения:

x ®₁ y Û ù₁ x Ú₁ y (3.18) x ®_1’ y Û ù₁ x Ú₂ y (3.22)

x ®₂ y Û ₂ x Ú₁ y (3.19) x ®_2’ y Û ₂ x Ú₂ y (3.23)

x ®₃ y Û é₄ x Ú₁ y (3.20) x ®_3’ y Û é₄ x Ú₂ y (3.24)

x ®₄ y Û é₅ x Ú₁ y (3.21) x ®_4’ y Û é₅ x Ú₂ y (3.25)

Полученные операции имеют различную интерпретацию, которую довольно сложно выразить вербально. Попробуем вместо этого, пойти в обратном направлении, а именно, найти различные интерпретации операций логического следствия, а затем, построить или подобрать для них формальное определение.

В классической двузначной логике импликация должна быть истинной тогда и только тогда, когда следствие всегда имеет место, если имеет место предпосылка. Если говорить в терминах семантики возможных миров, импликация истинна в тех мирах, где: либо выполняется и следствие и посылка, либо только следствие, либо ничего. Если пойти дальше, можно прийти к интерпретации с точки зрения теории множеств. Истинность любой формулы А ограничивает универсум возможных значений до некоторого множества N, и если A₁ ® A₂, то N₁ Ì N₂. Так, общезначимая формула не ограничивает универсум, поэтому может являться предпосылкой только другой общезначимой, и наоборот, тождественно ложная формула имеет в качестве допустимых значений пустое множество и, поэтому, ее следствием может выступать что угодно. К сожалению, такая интерпретация становится возможной для многозначной логики, только после выбора множества выделенных значений, поэтому поговорим о ней позже.

Рассмотрим импликацию, как следствие для обоих агентов. Эта импликация эквивалентна введенной ранее импликации ®₁. Её таблица истинности будет выглядеть так:

Таблица 3.8. Импликация как следствие для обоих агентов в логике L_min

х®1y	T	I	E	F
T	T	I	E	F
I	T	T	E	E
E	T	I	T	I
F	T	T	T	T

Рассмотрим импликацию как следствие для первого агента и как обратное следствие для второго. Смысл такого определения проявляется в логике спора. Её таблица истинности будет выглядеть так:

Таблица 3.9. Импликация как следствие для первого агента и обратное следствие для второго агента в логике L_min

х®5y	T	I	E	F
T	T	T	E	E
I	I	T	E	E
E	T	T	T	T
F	I	T	I	T

Этой операции не соответствует ни одно из определений (3.18)-(3.25). Её можно выразить следующим образом:

x ®₅ y = é₅ x ®₁é₅ y = ₁é₅ x Ú₁é₅ y = é₄ x Ú₁₂é₄₂ y (3.26)

Дальнейшее исследование логики L_dmin продолжим с построения аппарата логического вывода.

3.3.2. Вывод в четырехзначной диалоговой логике L_dmin

В предыдущем параграфе введена и описана четырехзначная диалоговая логика L_dmin, рассмотрены операции отрицания, конъюнкции, дизъюнкции, импликации и выявлены их свойства, также доказано, что система операций { ₂, ₃, Ú₁ } образует базис данной логики. Однако, этого недостаточно для практического применения, необходим эффективный механизм вывода и, в первую очередь, определения общезначимости формулы в логике L_dmin.

Проверять общезначимость можно различными способами, например, наиболее просто способ проверки заключается в использовании простого перебора. Очевидно, это не самый оптимальный способ. В качестве альтернативы используем метод, основанный на аналитических таблицах.

Для начала введём следующие определения.

Определение 3.14. Пусть X есть конечное множество атомарных формул X = { a, b, c …}, тогда однозначное соответствие s: X® L _{d min} называется сетапом, или единичным сетапом, здесь L_min= {T,F,I,E}.

Определение 3.15. Формула F является выполнимой в логике L_dmin, если существует такой сетап s, при котором F принимает значение T.

Определение 3.16. Формула F является общезначимой в логике L_dmin, если на любом сетапе s, F принимает значение T.

Определение 3.17. Формула F является внутренне выполнимой в логике L_dmin, если существует такой сетап s, при котором F принимает значение T или I.

Определение 3.18. Формула F является внутренне общезначимой в логике L_dmin, если на любом сетапе s, F принимает значение T или I.

Определение 3.19. Формула F является внешне выполнимой в логике L_dmin, если существует такой сетап s, при котором F принимает значение T или E.

Определение 3.20. Формула F является внешне общезначимой в логике L_dmin, если на любом сетапе s, F принимает значение T или E.

Очевидно, что формула общезначима тогда и только тогда, когда она общезначима и внутренне и внешне. Однако, и внешняя и внутренняя выполнимость формулы не гарантируют ее общую выполнимость.

Существует два варианта вывода на базе аналитических таблиц: с использованием означенных формул и без них. В диссертации используется вариант с использованием означенных формул.

Определение 3.21. Означенная формула – это запись вида FX, TX, IX или EX, где X - формула.

В классическом методе аналитических таблиц TX читается как “ X – истина”, а FX “ X – ложь”. Аналитическая таблица – это дерево с означенными формулами в качестве подписей в узлах дерева. В корне дерева находится исходная означенная формула. Ветви дерева получаются декомпозицией формулы, выполняемой по определенным правилам.

В классической логике если формула X выводима (общезначима), то она не может быть ложью. При доказательстве формулы табличным способом первоначально формула X отвергается. Для того, чтобы доказать некоторую формулу X, ей приписывается ложное значение (FX), после чего строится дерева вывода для FX с целью получить противоречие. Если противоречие получено, формула X считается доказанной. Критерием противоречия является замкнутость дерева вывода. Ветвь дерева называется замкнутой, если она содержит одновременно FA и TA, где A – некоторая подформула исходной формулы X. Если все ветви дерева формулы FX являются замкнутыми, то дерево вывода является замкнутым.

В методе аналитических таблиц для классической логики применяются следующие правила построения подветок: если встречается T(XÙY), то образуется два новых элемента ветви TX и TY. В случае, если встречается F(XÙY), ветвь расщепляется на две, в одной из которых добавляется FX, в другой FY.

При построении метода вывода на базе аналитических таблиц для четырехзначных логик важно определить способ означивания формул и дать критерий замкнутости дерева вывода.

Определение 3.22. Дерево вывода означенной формулы X, это граф (G,V) связностью 1, каждая вершина которого помечена означенной формулой, таким образом, что потомками каждой вершины являются вершины, помеченные формулами получающимися при декомпозиции означенной формулы, находящийся в вершине дерева.

Означенная формула Y является декомпозицией означенной формулы Х, YrX, тогда и только тогда когда получена из Х при помощи правил декомпозиции. Существует четыре типа правил: a-правила, b-правила, g-правила и d-правила аналогичные правилам для логики Белнапа, предложенным Фиттингом (см.[140]).

a		b		g		d
a1		b1		g1	g3	g4		d1	d3	d5	d6
		b2		g2	g1	g2		d2	d4

a	a1		a	a1		b	b1	b2
T2X	TX		Té4X	IX		F XÚ1Y	FX	FY
I2X	EX		Ié4X	TX
E2X	IX		Eé4X	FX
F2X	FX		Fé4X	EX

g	g1	g2	g3	g4
I XÚ1Y	IX	IY	FY	FX
E XÚ1Y	EX	EY	FY	FX

d	d1	d2	d3	d4	d5	d6
T XÚ1Y	IX	EY	EX	IY	TX	TY

Рис 3.3. Правила декомпозиции базисных функций в логике L_dmin

Так как операции { ₂, é₄, Ú₁ } образуют базис в L_dmin, то набор приведенных выше правил достаточен для декомпозиции произвольной формулы L_dmin. Для удобства использования можно аналогичным образом построить правила вывода для производных операций (см. рис 3.4).

a	a1		a	a1		b	b1	b2
Tù1X	FX		Té5X	EX		T XÙ1Y	TX	TY
Iù1X	EX		Ié5X	FX		E XÚ2Y	EX	EY
Eù1X	IX		Eé5X	TX		I XÙ2Y	IX	IY
Fù1X	TX		Fé5X	IX		F X®1Y	TX	FY

g	g1	g2	g3	g4
I XÙ1Y	IX	IY	TY	TX
E XÙ1Y	EX	EY	TY	TX
T XÚ2Y	TX	TY	EY	EX
F XÚ2Y	FX	FY	EY	EX
T XÙ2Y	TX	TY	IY	IX
F XÙ2Y	FX	FY	IY	IX
E X®1Y	IX	EY	FY	TX
I X®1Y	EX	IY	FY	TX

d	d1	d2	d3	d4	d5	d6
F XÙ1Y	IX	EY	EX	IY	FX	FY
I XÚ2Y	TX	FY	FX	TY	IX	IY
E XÙ2Y	TX	FY	FX	TY	EX	EY
T X®1Y	IX	IY	EX	EY	FX	TY

Рис 3.4. Правила декомпозиции производных функций в логике L_dmin

Определим отношение декомпозиции r.

Пусть x и y – ППФ L_dmin, тогда xry тогда и только тогда когда:

или x соответствует a, y соответствует a₁, в a-правиле,

или x соответствует b, y соответствует b₁, в b-правиле,

или x соответствует b₁, y соответствует b₂, в b-правиле,

или x соответствует g, y соответствует g₁, в g-правиле,

или x соответствует g, y соответствует g₃, в g-правиле,

или x соответствует g, y соответствует g₄, в g-правиле,

или x соответствует g₁, y соответствует g₂, в g-правиле,

или x соответствует g₃, y соответствует g₁, в g-правиле,

или x соответствует g₄, y соответствует g₂, в g-правиле.

Лемма 3.4 Для любой ППФ L_dmin существует дерево вывода.

Доказательство. Существует единственное правило декомпозиции (см. 3.3) для любой связки из множества { ₂, é₄, Ú₁ } и любого значения формулы, т.е. для любой означенной формулы вида D ₂ F₁, D é₄ F₁, DF₁ Ú₁ F₂, где DÎ{T,F,E,I}, F₁,F₂ÎППФ L_dmin, существует единственное правило декомпозиции, применив которое мы уменьшаем количество логических связок на 1, в конечном итоге неизбежно перейдем к атомарным формулам, которые не могут быть далее разложены по правилам декомпозиции, но которые выражают ограничения на значение соответствующих переменных.

Определение 3.23. Ветвь дерева вывода называется замкнутой, если в ней существуют две вершины, помеченные одинаковыми формулами, означенными различным образом.

Определение 3.24. Дерево вывода означенной формулы X, является замкнутым тогда и только тогда, когда каждая его ветвь замкнута.

Ветвь дерева вывода означенной формулы DX означает набор значений, которые должны принимать подформулы, чтобы формула принимала указанное значение. Причем, если из одной вершины выходит несколько ветвей, это означает, что возможны различные наборы значений подформул. Замкнутость ветви означает противоречивость требований, накладываемых на некоторую подформулу, которая должна одновременно принимать несколько различных значений. Замкнутость дерева вывода означенной формулы DX означает невозможность формулы принимать значение D.

В связи с этим, для определения возможных значений формулы необходимо построить деревья вывода для всех вариантов означивания и определить их замкнутость.

Таблица 3.10. Результаты вывода для формулы Х методом аналитических таблиц.

TX	FX	IX	EX	Результат
не замкнуто	замкнуто	замкнуто	замкнуто	Х тождественно истинно (всегда принимает значение T)
замкнуто	не замкнуто	замкнуто	замкнуто	Х тождественно ложно (всегда принимает значение F)
замкнуто	замкнуто	не замкнуто	замкнуто	Х тождественно внутренне истинно (всегда принимает значение I)
замкнуто	замкнуто	замкнуто	не замкнуто	Х тождественно внешне истинно (всегда принимает значение E)
не замкнуто	не замкнуто	замкнуто	замкнуто	Х тождественно согласно (всегда принимает значение T или F)
замкнуто	замкнуто	не замкнуто	не замкнуто	Х тождественно спорно (всегда принимает значение I или E)
не замкнуто	замкнуто	не замкнуто	замкнуто	Х тождественно истинно для первого агента (всегда принимает значение T или I)
не замкнуто	замкнуто	замкнуто	не замкнуто	Х тождественно истинно для второго агента (всегда принимает значение T или E)
замкнуто	не замкнуто	замкнуто	не замкнуто	Х тождественно ложно для первого агента (всегда принимает значение F или E)
замкнуто	не замкнуто	не замкнуто	замкнуто	Х тождественно ложно для второго агента (всегда принимает значение F или I)
не замкнуто	не замкнуто	не замкнуто	не замкнуто	Х полностью неопределенно (может принимать любые значения)
замкнуто	не замкнуто	не замкнуто	не замкнуто	Х частично неопределенно (X не может принимать значение T)
не замкнуто	замкнуто	не замкнуто	не замкнуто	Х частично неопределенно (X не может принимать значение F)
не замкнуто	не замкнуто	замкнуто	не замкнуто	Х частично неопределенно (X не может принимать значение I)
не замкнуто	не замкнуто	не замкнуто	замкнуто	Х частично неопределенно (X не может принимать значение E)

Приведем пример вывода при помощи аналитических таблиц в L_dmin. Пусть дана формула é₄A Ú₁₂é₄₂A, докажем что она является тавтологией.

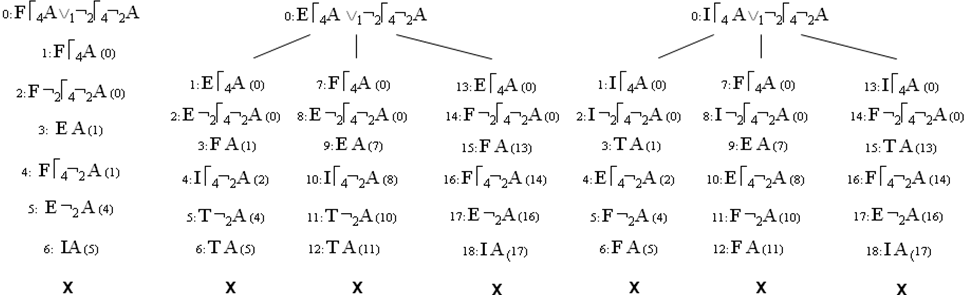
Рис 3.5. Пример вывода при помощи аналитических таблиц в L_dmin.

Как видим на рис 3.5, все деревья для означиваний F, E и I являются замкнутыми. Следовательно, формула é₄A Ú₁₂é₄₂A может принимать только значение T, т.е. é₄A Ú₁₂é₄₂A – тождественно истинна.

3.4. Диалоговое произведение логик и вывод на нем.

Приведённое выше построение механизма вывода для L_dmin, удобно для описания логики малой размерности, однако, с увеличением мощности множества истинностных значений конструирование и использование правил вывода для каждого случая становится достаточно трудоемким.

В связи с этим рассмотрим подход, связанный с определением вывода в произведении логик через композицию выводов в базовых логиках. Рассмотрим две логики L₁ и L₂ (мы подразумеваем, что этими логиками пользуются два разных агента – участника диалога). Пусть существует формула F, она является тавтологией (тождественно истинна) в логиках обоих агентов, будет ли она тавтологией в логике L₁´L₂?

Для начала введём несколько определений.

Определение 3.25. Операция j, определенная[1] на L₁´L₂ является дистрибутивной относительно декартова произведения логик, если существуют такие j₁^* и j₂^*, что j(<x₁,y₁>,<x₂,y₂>,…,<x_n,y_n>) = <j₁^*(x₁,x₂,…,x_n), j₂^*(y₁,y₂,…,y_n)>.

Определение 3.26. Диалоговым произведением L₁°L₂ логик L₁ и L₂ назовём следующее отображение

°: (L₁,{j₁,…,j_n},T₁)´(L₂,{y₁,…,y_m},T₂) ® (L₁´L₂,{j₁^*,…,j_k^*},T₁´T₂), такое что {f₁^*,…,f_k^*} – базис для функций, дистрибутивных относительно L₁´L₂.

Лемма 3.4. Для любой формулы Ф, составленной из связок, дистрибутивных относительно L₁´L₂, существует эквивалентное представление <Ф₁,Ф₂>.

Доказательство весьма тривиально. Согласно определению диалогового произведения, любую k-арную связку j_i^*, можно представить в виде j_i^*(<x₁,y₁>,<x₂,y₂>,…,<x_k,y_k>) = <j_i^’(x₁,x₂,…,x_k), j_i^’’(y₁,y₂,…,y_k)>. Если все <x₁,y₁>,<x₂,y₂>,…,<x_k,y_k> - атомарны, то лемма выполняется для случая произвольной формулы с одной связкой.

Дата добавления: 2015-09-04