
Читайте также:
|
Получим аналитические выражения для АЧХ и ФЧХ.
Частотная передаточная функция апериодического звена (после подстановки в передаточную функцию p=jω):
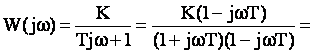
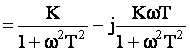
Таким образом, вещественная частотная характеристика:
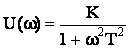
Мнимая частотная характеристика:
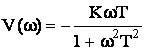
Амплитудная частотная характеристика:
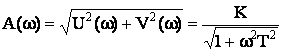
Фазовая частотная характеристика:
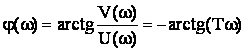
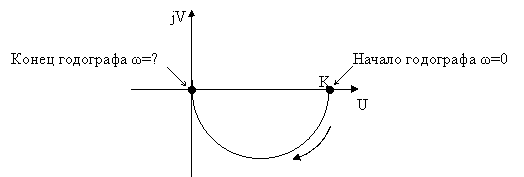
АФЧХ
Годограф Найквиста для апериодического звена имеет вид полуокружности.
|
Дата добавления: 2015-09-04; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнение звена | | | ЛАЧХ и ЛФЧХ |