Интегрирующее звено

Передаточная функция:

.

Если входная и выходная величина одной размерности, то передаточную функцию обычно записывают в виде:

,

где Т – постоянная времени (в секундах).

Уравнение звена:

или .

Выходная величина пропорциональна интегралу входной величины.

Статическая характеристика: y_ст =W(0)·x_ст, где W(0) = ∞

Это значит, что статический режим невозможен при x_ст 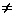0, т.к. звено непрерывно интегрирует входную величину и выходная величина непрерывно изменяется. Статический режим возможен только при x_ст=0, когда интегрирование прекращается. Таким образом, статическая характеристика совпадает с осью y.

Переходная функция: h(t)=K·t·1(t)

Ее значение линейно нарастает во времени (теоретически до бесконечности). Скорость нарастания переходной функции равна коэффициенту К.

Весовая функция: g(t)=K·1(t)

Интегрирующее звено обладает способностью сохранять постоянное не равное нулю значение выходной величины при равенстве нулю входной величины.

Пример: реакция интегрирующего звена на сложное ступенчатое воздействие.

ЛАЧХ:

В логарифмическом масштабе частоты это уравнение прямой линии с наклоном –20 дБ/дек. С увеличением частоты значение ЛАЧХ уменьшается.

При ω<K, L>0 – звено усиливает амплитуду.

При ω=K, L=0 – амплитуды входной и выходной величины одинаковы.

При ω>K, L<0 – звено ослабляет амплитуду.

ЛАЧХ пересекает ось частоты на частоте ω=К (ω=1/Т). На частоте ω=1 значение ЛАЧХ равно 20·lg(К).

ЛФЧХ: φ(ω)= – 90˚ = – π/2 рад

Интегрирующее звено при любой частоте гармонического воздействия вносит отставание по фазе на четверть периода.

Пример ЛАЧХ и ЛФЧХ интегрирующего звена для К>1.

Дата добавления: 2015-09-04