Колебательное звено

Передаточная функция: ,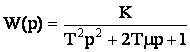

где К – статический коэффициент передачи [К=W(0)], Т – постоянная времени (единица измерения – секунды), μ – коэффициент демпфирования (безразмерная величина), находится в пределах0<μ<1.

Свойства колебательного звена зависят от значения полюсов его передаточной функции, т.е. от корней уравнения:

.

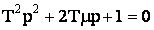При 0<μ<1 получим два комплексно-сопряженных корня.

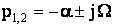, где , .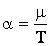

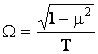Уравнение звена:

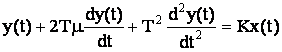
Переходная функция колебательного звена описывается формулой:

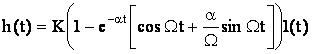
Колебательный характер переходной функции определяется наличием в ней периодических функций синуса и косинуса. Колебания будут затухать с течением времени, т.к. множитель при этих функциях 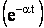уменьшается с увеличением времени и стремится к нулю при (t→∞).

В автоматических системах различают свободные и вынужденные колебания. Вынужденные колебания выходной величины звена возникают из-за колебаний воздействия (например, при синусоидальном воздействии). Колебания переходной функции колебательного звена – это свободные колебания: воздействие на звено не периодическое, а колебания возникают из-за собственных колебательных свойств звена.

Можно сделать следующие выводы о виде переходной функции:

1) Установившееся значение переходной функции равно К:

.

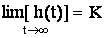2) Модуль мнимой части полюсов передаточной функции Ω представляет собой угловую частоту колебаний. Период колебаний равен 2π/ω.

3) Модуль действительной части полюсов передаточной функции α определяет скорость затухания колебаний. Чем больше α, тем быстрее затухают колебания. При одной и той же постоянной времени Т колебания будут затухать тем быстрее, чем больше значение коэффициента демпфирования μ.

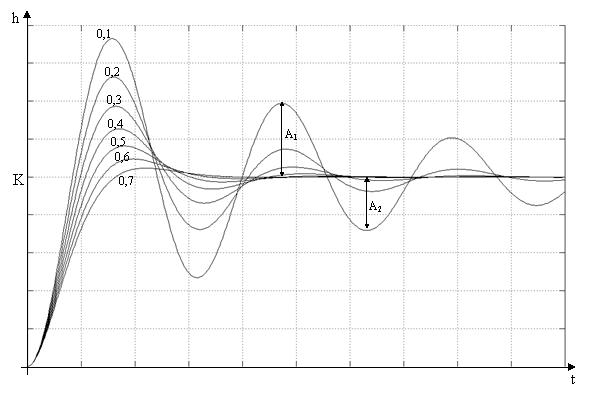
Рассмотрим графики переходных функций колебательного звена при одних и тех же К и Т и разных коэффициентах демпфирования μ (0,7…0,1). Чем меньше μ тем выше амплитуда колебаний и больше время их затухания.

Амплитуда колебаний отсчитывается от уровня установившегося значения К. Отношение любых двух соседних полуволн колебаний всегда постоянно и равно:

.

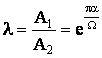Параметр λ называется декрементом затухания колебаний.

Рассмотрим вид переходной функции при граничных значениях коэффициента демпфирования μ=1 и μ=0.

При μ=1 мнимая часть полюсов обращается в ноль. Звено имеет два одинаковых действительных полюса. Это будет уже не колебательное звено, а апериодическое звено второго порядка. Переходная функция при μ=1 будет монотонной:

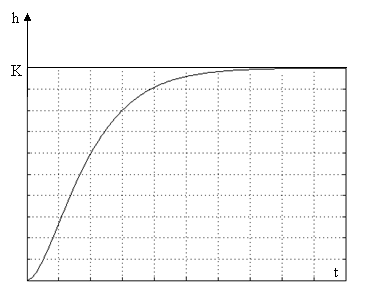
При μ=0 получим звено, называемое консервативным. Передаточная функция консервативного звена:

.

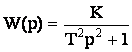При μ=0 действительная часть полюсов передаточной функции оказывается равной нулю:

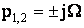, где .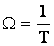

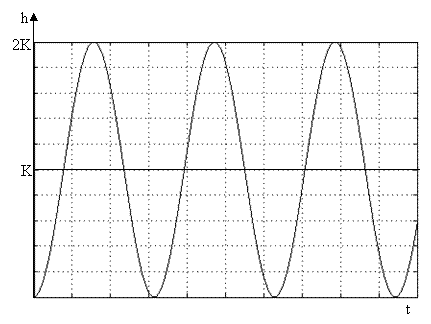
Поскольку α=0, множитель е^–αt в переходной функции превращается в единицу. Колебания переходной функции консервативного звена будут незатухающими и продолжаются (теоретически) бесконечно долго. Угловая частота этих колебаний равна (1/Т), период колебаний равен (2πT). Амплитуда колебаний будет постоянна и равна К. Декремент затухания: λ=1.

Дата добавления: 2015-09-04