Внутренняя энергия и энтропия газа Ван-дер-Ваальса

Внутренняя энергия идеального газа не зависит от объема. Это верно для идеальных газов, но не для реальных, внутренняя энергия которых зависит и от T, и от V.

Для определения вида функции E (T, V) для газа Ван-дер-Ваальса подставим (3) в соотношение (1.52), которое после этого принимает вид

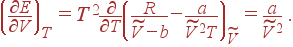
(11)

Интегрируя (11) по V при T = const, получаем

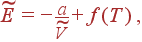
где функция f (T) не зависит от 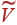. Член 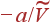представляет потенциальную энергию взаимодействия молекул.

Чтобы найти функцию f (T), нужно знать зависимость теплоемкости газа от температуры. Примем, что теплоемкость при постоянном объеме не зависит от T: C_V = const. Тогда из формулы для C_V следует

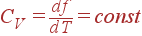
и, следовательно,

f (T) = C_VT + f ₀.

В результате выражение для 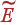принимает вид

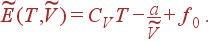
(12)

Вычислим теперь энтропию газа Ван-дер-Ваальса. Для этого в основное термодинамическое тождество, разрешенное относительно 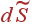и записанное в форме (1.55), подставим (12) и (3):

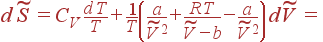
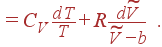
(13)

Нетрудно проверить, что выражение в правой части (13) представляет полный дифференциал функции от T и 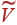. Интегрирование (13) дает

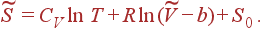
(14)

Выражение (12) содержит константу a и не содержит константы b. Другими словами, внутренняя энергия газа зависит от взаимодействия между его молекулами, но не от их размеров.

Напротив, выражение (14) содержит константу b, но не содержит a. Это имеет тот физический смысл, что степень беспорядка в системе, характеризуемая величиной энтропии, не зависит от межмолекулярного взаимодействия, но уменьшается с ростом объема молекул. Последнее связано с тем, что для движения молекул доступна только та часть полного объема газа, которая не занята другими молекулами.

Дата добавления: 2015-09-02