Эффект Джоуля – Томсона для газа Ван-дер-Ваальса

Рассмотрим особенности охлаждения или нагревания реального газа в процессе Джоуля – Томсона на примере газа Ван-дер-Ваальса. Для простоты примем, что масса газа составляет один моль. Прежде всего найдем выражение для производной , которая входит в формулу (28) для коэффициента Джоуля – Томсона. Для этого продифференцируем обе части уравнения (3) по T при P = const, полагая 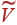функцией T. В результате получаем уравнение

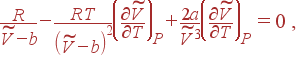
откуда

(31)

Подставим теперь (31) в (28). Имеем

или

(32)

Таким образом, коэффициент Джоуля – Томсона обращается в нуль при условии

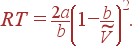
(33)

При использовании приведенных переменных (8) это условие принимает вид

(34)

Если разрешить (34) относительно переменной v и подставить в (10), то получается уравнение инверсии

(35)

решение которого имеет вид

(36)

Наконец, возвращаясь к переменным T и P, приходим к следующей формуле для температуры инверсии

(37)

Эта формула определяет кривую инверсии на (T, P) диаграмме, которая имеет куполообразную форму (рис. 11). Область положительного эффекта Джоуля – Томсона находится под кривой.

Из формулы (37) видно, что при P < 9 P_k имеется две точки инверсии, различие между которыми уменьшается с ростом P. При P = 9 P_k верхняя и нижняя точки инверсии сливаются в одну точку

Ti 0 = 3 Tk.

(38)

Для большинства газов нижняя точка инверсии лежит в области жидкого состояния, и ее рассмотрение не представляет интереса.

Максимальная температура инверсии, соответствующая , согласно (37) равна

(39)

Это соотношение приближенно выполняется для большинства газов. Так, для кислорода T_{i max} составляет 893 K а T_k – 154 K. Для водорода T_{i max} = 205 K, а T_k = 33 K. Для гелия T_{i max} = 40 K, а T_k = 4,2 K. Из этих данных следует, что при нормальных температурах водород и гелий нагреваются в процессе Джоуля – Томсона. Поэтому для сжижения их нужно предварительно охладить до температуры ниже температуры инверсии.

Вопросы

1. Изобразите в координатах Р – V изотерму конденсации однокомпонентного идеального газа.
2. Почему в однокомпонентной системе в течение всего процесса конденсации давление в системе сохраняется постоянным?
3. В чем заключается принцип соответственных состояний? Кто его впервые сформулировал?
4. Суть эксперимента Джоуля-Томсона и его результаты.
5. Как ведет себя энтальпия в процессе Джоуля-Томсона?
6. В чем заключается эффект Джоуля-Томсона?
7. Напишите выражение для дифференциального коэффициента Джоуля-Томсона.
8. Чему равен коэффициент Джоуля-Томсона для идеального газа?
9. Чему равен коэффициент Джоуля-Томсона для реального газа?
10. В чем смысл кривой инверсии?

Дата добавления: 2015-09-02