Критическая точка. Закон соответственных состояний

Рассмотрим теперь критическую точку K. Критические значения T_k, V_k и P_k можно выразить через параметры a и b, входящие в уравнение Ван-дер-Ваальса. Для этого учтем то обстоятельство, что критическая изотерма, соответствующая T = T_k, имеет горизонтальную точку перегиба K. Другими словами, при V = V_k

(2)

Перепишем (1) в форме

(3)

и дважды продифференцируем его по 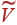. Тогда условия (2) приводят к уравнениям

(4)

Деля правую и левую части первого уравнения на соответствующие части второго, получаем , откуда

(5)

Подставляя (5) в одно из уравнений (4), находим

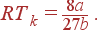
(6)

Наконец, для нахождения P_k подставляем (5) и (6) в (3), что дает

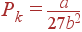
(7)

Если выразить температуру, объем и давление в единицах T_k, V_k и P_k, то уравнение Ван-дер-Ваальса принимает форму, одинаковую для всех веществ. Вводя приведенные переменные

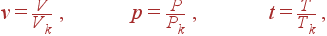
(8)

представим уравнение (1) в виде

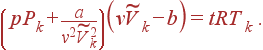
(9)

Подставляя теперь явные выражения для 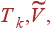и P_k в (9), получаем

(10)

Уравнение (10) не содержит констант a и b, характеризующих конкретное вещество. Это означает, что оно является универсальным, т.е. справедливо для всех веществ. Из (10) следует, что если из трех приведенных переменных (8) две переменные одинаковы для двух веществ, то и третья переменная также одинакова. Этот закон называется законом соответственных состояний. Он выражает тот факт, что при использовании приведенных переменных можно совместить изотермы всех веществ. Закон позволяет находить изотермы различных газов по измеренным значениям их критических параметров и известным изотермам других газов.

Дата добавления: 2015-09-02