Гусева Т.С., Остапенко Е.С., Кулиев В.Д., Бутова О.Н.

§1. В.Д. Кулиевым предложен следующий метод суммирования рядов. Рассмотрим ряд

Если функция f(z) регулярна в правой полуплоскости Re z≥m, z -плоскости и такова, что ее модуль при 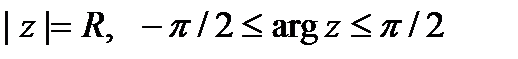при достаточно больших R может быть как мал, так и велик, то для суммирования рядов такого типа метод Плана не применим. Поэтому возникает необходимость в разработке метода суммирования рядов, учитывающего и это обстоятельство.

Обозначение. Под S_α понимается сектор, образованный двумя лучами в z -плоскости, исходящими из точки O₁(m,0) симметрично относительно действительной оси под углом α (0<α≤π/2).

Теорема Кулиева. Пусть:

1°. Функция f(z) регулярна внутри и на границе сектора S_α.

2°. Функция f(z) в точках z=k, где k=m, m+1, m+2,…, не имеет нулей.

3°. Угол α такой, что предельное равенство

(1.1)

выполняется равномерно по

4°. Несобственный интеграл

(1.2)

сходится.

Тогда

(1.3)

где

Этот метод в дальнейшем назовем - метод.

§2. Рассмотрим задачу без начальных условий.

Если процесс теплопроводности рассматривается в момент, достаточно далеко отстоящий от начального, то влияние начальных условий практически не сказывается на распределении температуры в момент наблюдения. В этом случае ставится задача об отыскании решения однородного уравнения теплопроводности, удовлетворяющего граничным условиям одного из трех основных типов, задаваемых для всех .

Рассмотрим первую краевую задачу для полубесконечного стержня, с теплоизолированной боковой поверхностью.

Требуется найти ограниченное решение однородного уравнения теплопроводности при 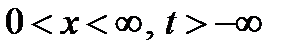, удовлетворяющее условию где - заданная функция. Предполагается, что функции и ограничены всюду, т.е. , 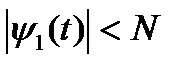(M, N – константы).

Распределение температуры можно записать так:

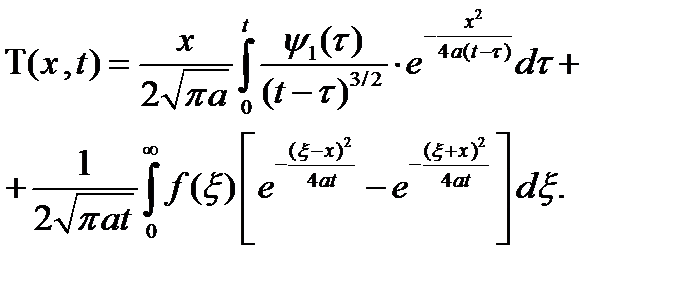(2.1)

Тогда ограниченное решение однородного уравнения теплопроводности при 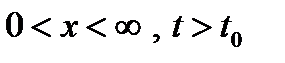, удовлетворяющее условиям , , 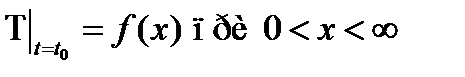представляет собой следующую сумму двух слагаемых

(2.2)

Покажем, что второе слагаемое в пределе при дает нуль

(2.3)

В самом деле, так как по условию , то имеем следующую оценку

откуда при и фиксированных x и t следует утверждение (2.3). Теперь предельный переход при , в выражении (2.2) дает нам искомое решение задачи:

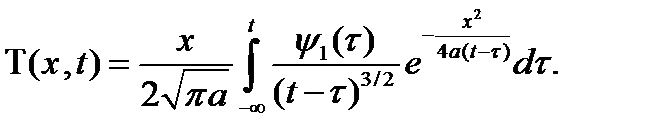(2.4)

Полезное представление полученного решения получим, если ввести в (2.4) новую переменную интегрирования :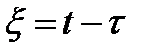

(2.5)

Рассмотрим с его помощью один из наиболее часто встречающихся случаев граничного условия – периодическое условие вида

(2.6)

Эта задача изучалась еще Фурье и впервые была применена при определении температурных колебаний почвы [ ].

Учитывая (2.6) в (2.3), получаем

где - функция Макдональда.

Отсюда, учитывая, что

окончательно находим

(2.7)

Это решение другим способом получено в [ ].

Поскольку одномерное уравнение теплопроводности формально совпадает с уравнением

(2.8)

определяющим движение вязкой жидкости над колеблющейся плоскостью, то решению уравнения (2.8), удовлетворяющему условию 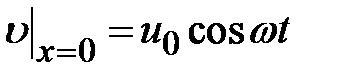можно сразу написать по аналогии формулой (2.7) в виде

Здесь - кинематическая вязкость.

Таким образом, в вязкой жидкости могут существовать поперечные волны: скорость 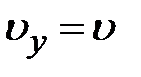перпендикулярна направлению распространения волны. Они, однако, быстро затухают по мере удаления от создающей их колеблющейся твердой поверхности. Затухание амплитуды происходит по экспоненциальному закону с глубиной проникновения . Эта глубина падает с увеличением частоты волны и растет с увеличением вязкости жидкости.

Замечание. -метод суммирования может быть успешно применен к решению задачи о свободных малых колебаниях струны с закрепленными концами и заданными начальными положениями и начальными скоростями её точек. Здесь на этом не будем останавливаться.

Список литературы:

1. Кулиев В.Д. Сингулярные краевые задачи. М.: ФИЗМАТЛИТ, 2005.

Дата добавления: 2015-09-01