Некоторые утверждения и примеры

Следует указать, что справедливы следующие утверждения:

1. Формула Лобачевского (1.2) остается в силе и в том случае, когда функция f(x) в промежутке интегрируема в несобственном смысле (при сохранении прочих условий теоремы 1 Лобачевского).

2. Формула Лобачевского (1.4) и формула (1.5) также остаются в силе в том случае, когда функция f(x) в промежутке интегрируема в несобственном смысле (при сохранении прочих условий теоремы 2 Лобачевского и теоремы 3, если функция f(x) в точке непрерывна; если же функция f(x) в точке имеет интегрируемую особенность, то условие отпадает, а остальные условия теоремы 2 Лобачевского и теоремы 3 при этом сохраняются).

Следствие вышеперечисленных теорем:

1. Если 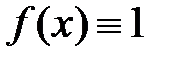, то из формулы Лобачевского (1.2) следует, что

(2.1)

2. Если , где m – любое целое число, то из (1.2) следует, что

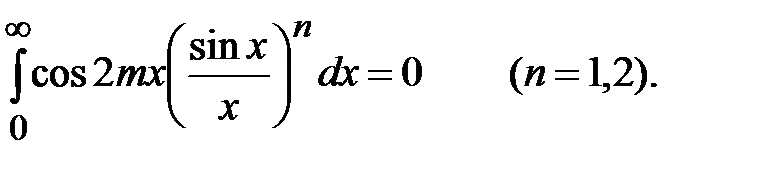
3. Если , то из (1.2) приходим к формулам Валлиса

~

~

4. Если 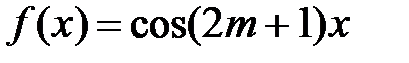, где m=0, ±1,…, то из (1.4) и (1.5) следует, что

Примеры.

1°. Рассмотрим интеграл

где Г(t) – гамма-функция Эйлера. Благодаря тому, что

интеграл допускает применение теоремы 2 и теорема 3 без труда вычисляется

Отметим, что при n=2 интеграл является частным случаем интеграла Рамануждана.

Теперь вычислим этот интеграл при n=2 с помощью теоремы 1 Лобачевского. Выполнив в интеграле

интегрирование по частям, получим

Чтобы вычислить этот интеграл при n=1, следует воспользоваться результатами теорем 1 и 2 Лобачевского. Вычисления дают

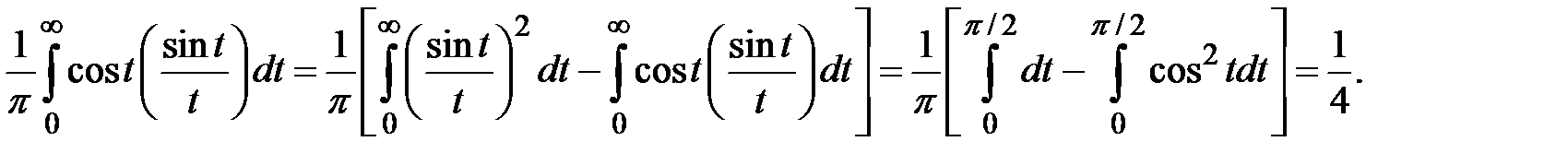
Отметим, что используя этот интеграл (при n=2) можно показать, что

Действительно,

откуда следует

Теперь остается учесть, что

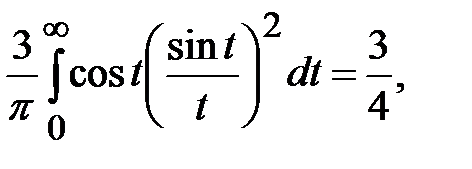
чтобы получить искомое равенство

Исходя из равенства

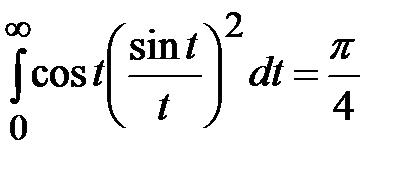
и выполнив в левой его части интегрирование по частям, находим значение еще одного интеграла

2°. С помощью теоремы Лобачевского докажем, что для любого конечного t

(2.2)

Доказательство. Сначала рассмотрим случай t>0. Имеем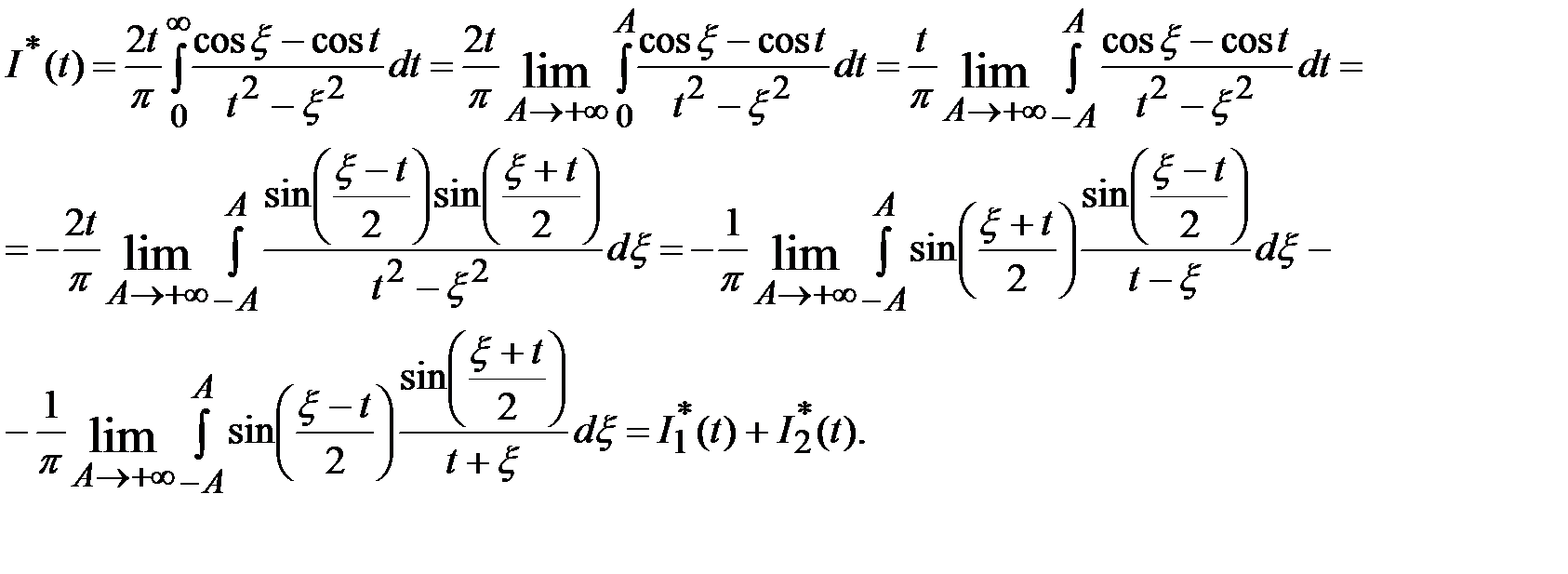

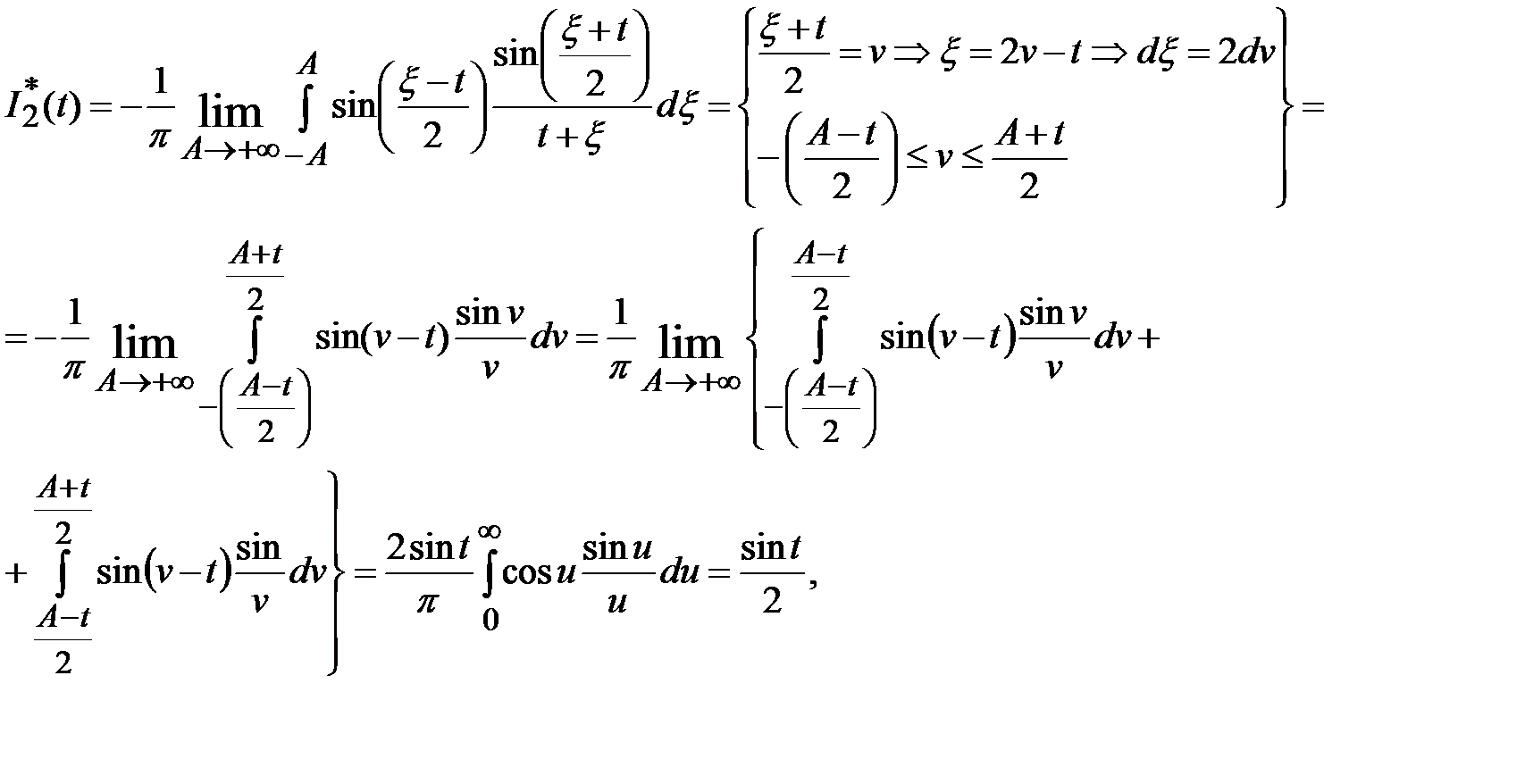
Аналогично доказывается случай t<0.

Пусть теперь t=0. Докажем, что в этом случае

Действительно,

Доказательство закончено.

Список литературы:

1. Н.И. Лобачевский. Полное собрание сочинений. ГИТТЛ. Москва-Ленинград, 1951.

Кулиев В.Д. Сингулярные краевые задачи. М.: ФИЗМАТЛИТ, 2005.

- МЕТОД СУММИРОВАНИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ БЕЗ НАЧАЛЬНОГО УСЛОВИЯ

Дата добавления: 2015-09-01