Теоремы Н.И. Лобачевского и новая теорема

Имеет место

Теорема 1. (Н.И. Лобачевский). Если функция f(x) 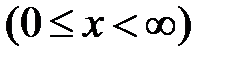удовлетворяет условиям

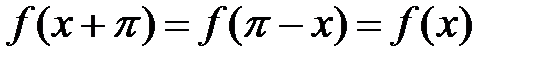(1.1)

и если существует интеграл

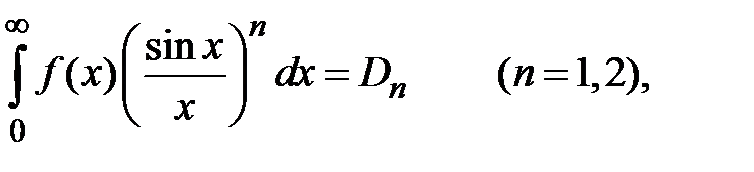
то

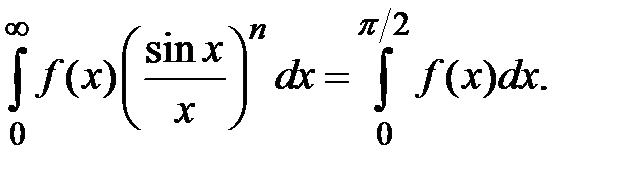(1.2)

Доказательство. Представим интеграл в виде суммы ряда

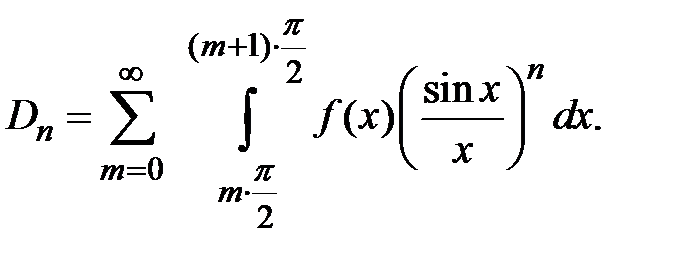
Пусть 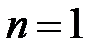. Положив 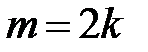или и прибегнув, соответственно, к подстановке 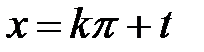или 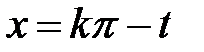, в силу (1.1), будем иметь:

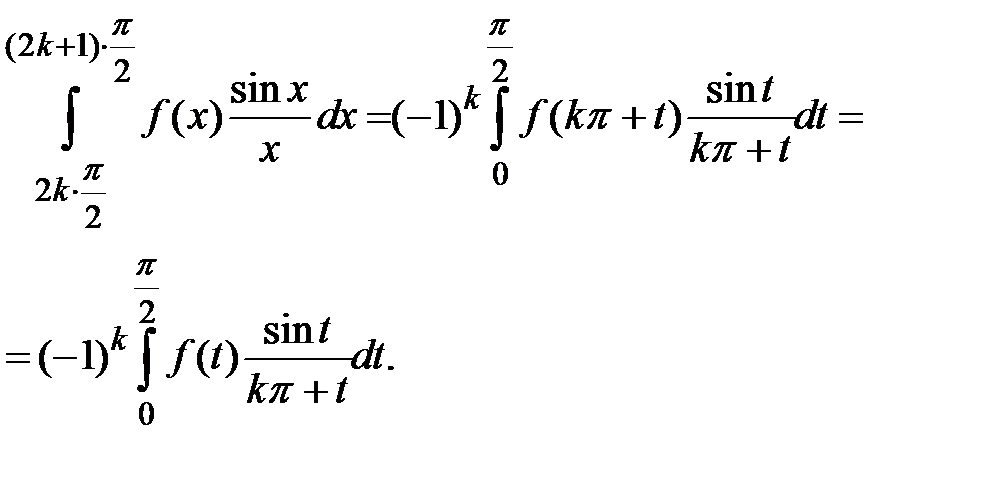
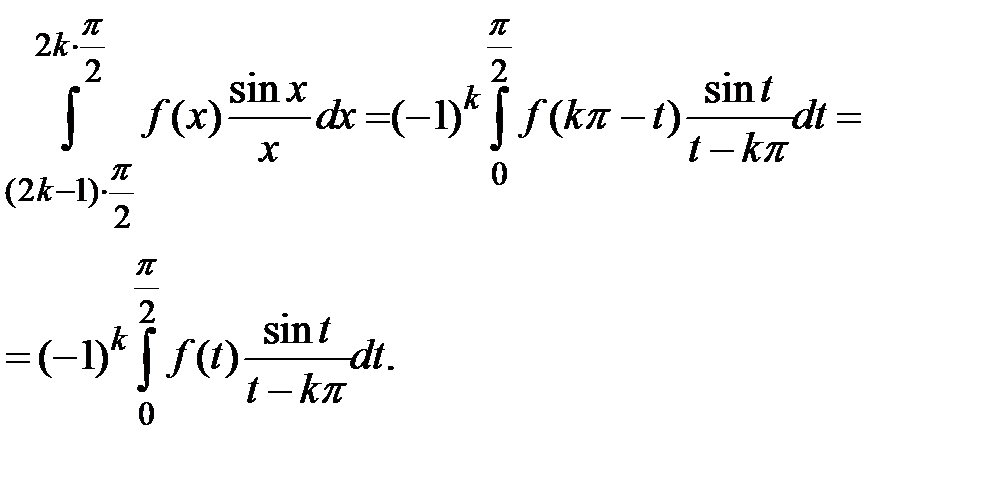
Отсюда

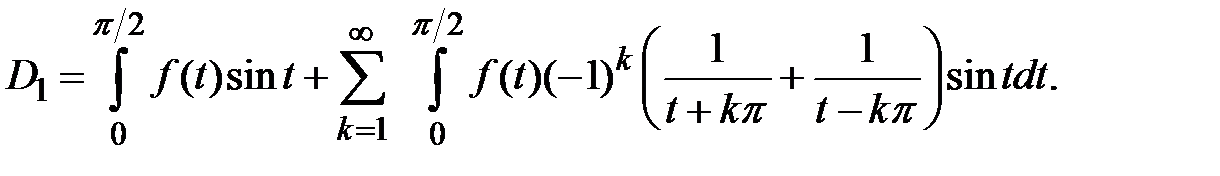
Так как ряд

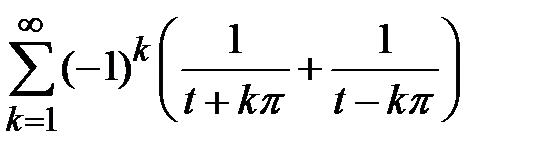
В промежутке 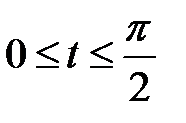сходится равномерно, ибо мажорируется сходящимся рядом

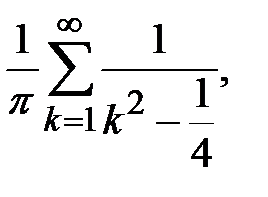
то его можно интегрировать почленно.

Следовательно,

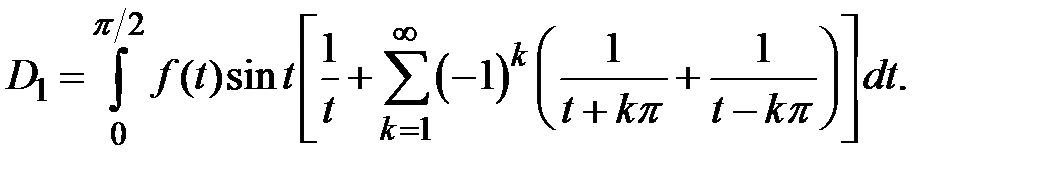
Но выражение в квадратных скобках есть разложение на простые дроби функции .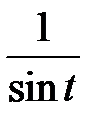

Таким образом, окончательно имеем

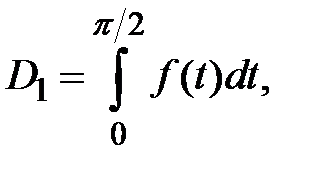
что и требовалось доказать для случая .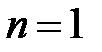

Пусть теперь 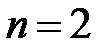. Поступая точно так же, как для случая 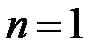, получаем

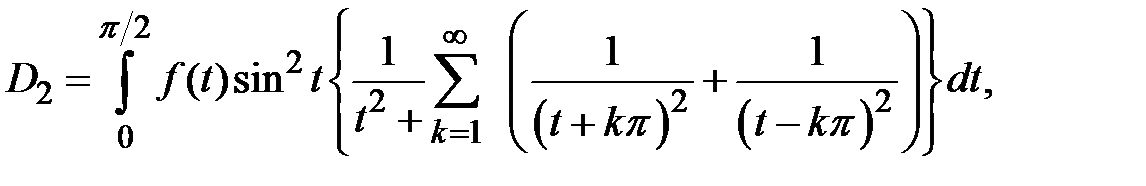
откуда замечая, что

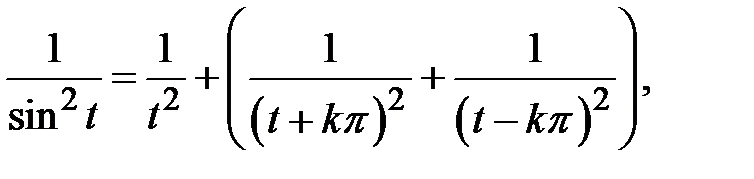
находим

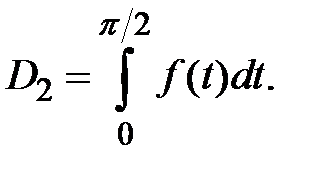
Теорема доказана.

Замечание 1. Определим сумму ряда

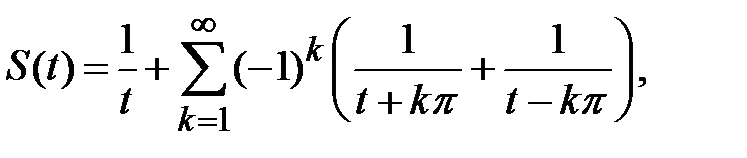
т.е. докажем, что

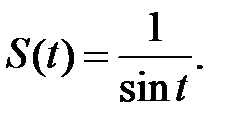
Функцию 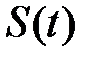можно представить в виде:

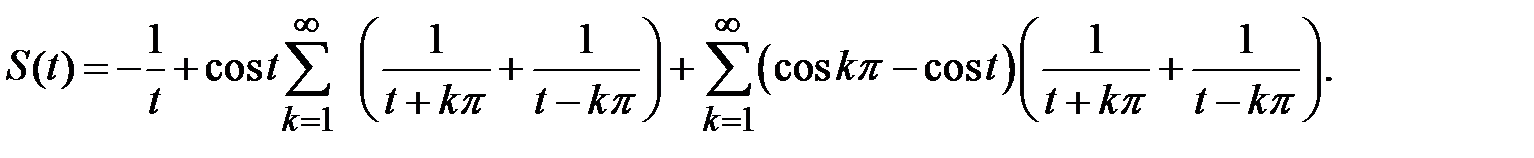
Последний ряд удовлетворяет всем требованиям формулы суммирования Плана [2].

Имеем

Замечая, что для любого конечного 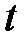(см. ниже (2.2)):

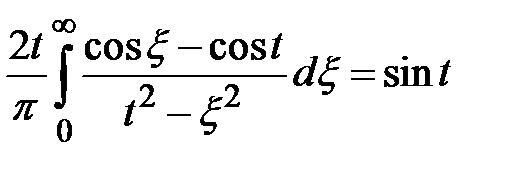
и

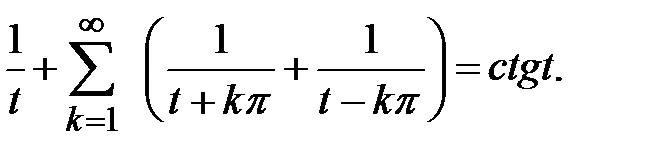
Окончательно, находим

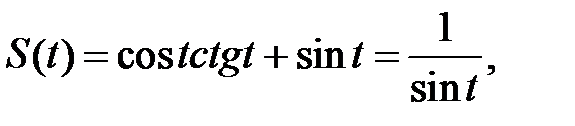
что и требовалось доказать.

Теорема 2. (Н.И. Лобачевский). Если функция f(x) удовлетворяет условиям

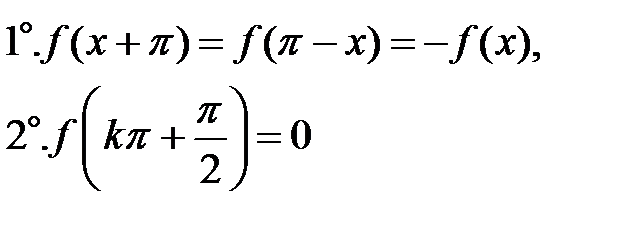(1.3)

(условия непрерывности функции 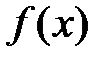в точках , где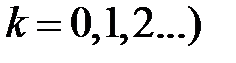

и если существует интеграл, то

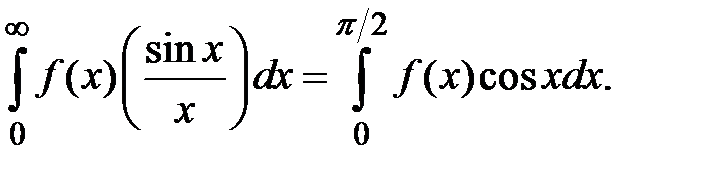(1.4)

Доказательство. Поступая точно так же, как при доказательстве теоремы 1 (Н.И. Лобачевский), получаем

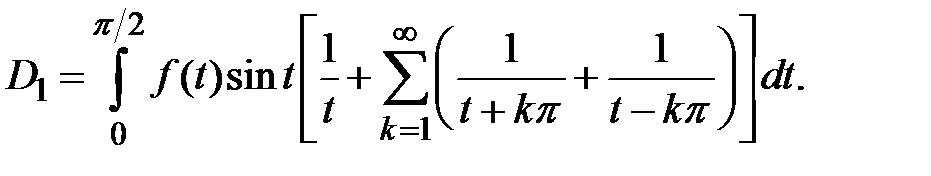
Отсюда, замечая, что

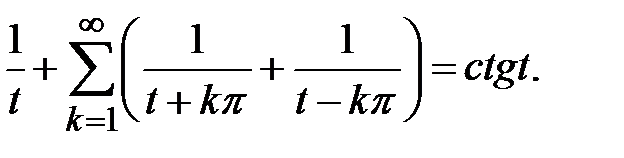
приходим к (1.4). Доказательство закончено.

Теорема 3. Если функция 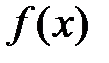удовлетворяет условиям теоремы 2 (Н.И. Лобачевский) и если существует интеграл

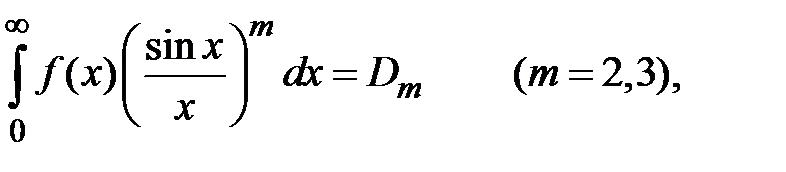
то

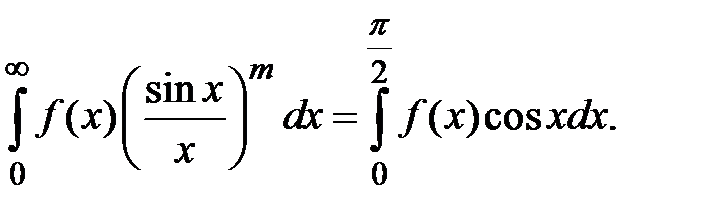(1.5)

Доказательство. Поступая точно так же, как при доказательстве теоремы 1 (Н.И.Лобачевский), в силу (1.3) получаем

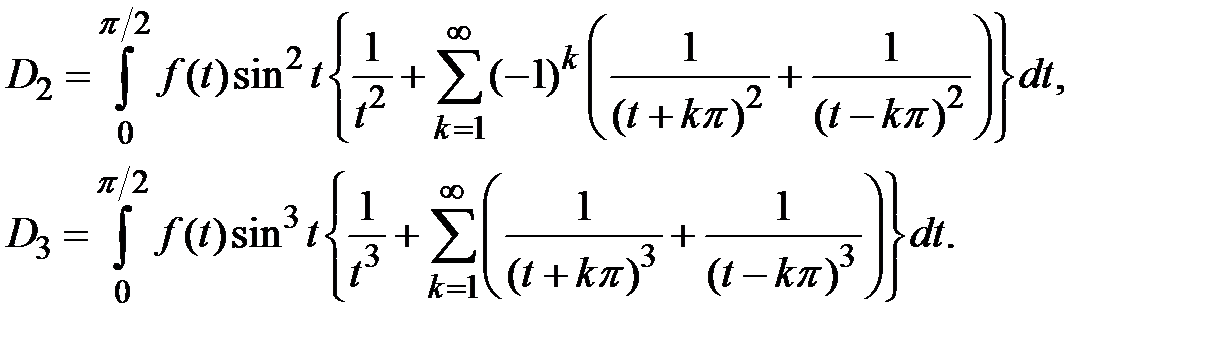
Отсюда, замечая, что

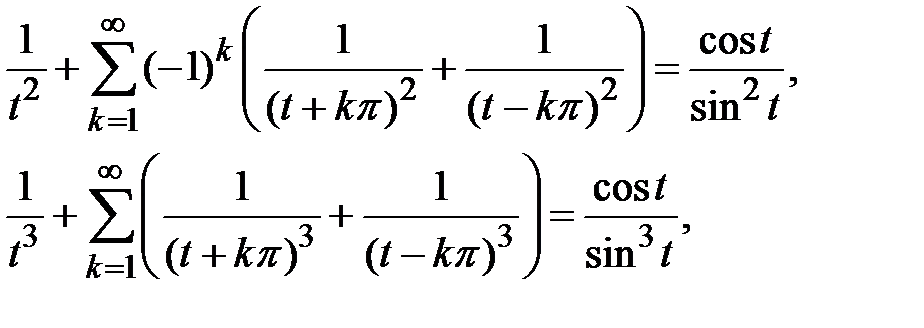
приходим к утверждению теоремы 3 (1.5).

Дата добавления: 2015-09-01