Кулиев В.Д., Юркова Е.А., Белова Т.А., Ветчинкин М.М.

§1. В.Д. Кулиевым предложен следующий метод суммирования рядов. Рассмотрим ряд

Если функция f(z) регулярна в правой полуплоскости Re z≥m, z -плоскости и такова, что ее модуль при 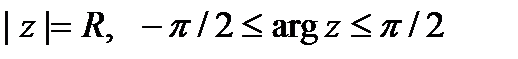при достаточно больших R может быть как мал, так и велик, то для суммирования рядов такого типа метод Плана не применим. Поэтому возникает необходимость в разработке метода суммирования рядов, учитывающего и это обстоятельство.

Обозначение. Под S_α понимается сектор, образованный двумя лучами в z -плоскости, исходящими из точки O₁(m,0) симметрично относительно действительной оси под углом α (0<α≤π/2) (см. рис. 1).

m+Re^iα

m+Re^-iα

n+1/2=R+m

τ

m

m+εe^-iα

m+εe^iα

m+ε

n

n+1

α

Рис. 1

Теорема Кулиева. Пусть:

1°. Функция f(z) регулярна внутри и на границе сектора S_α.

2°. Функция f(z) в точках z=k, где k=m, m+1, m+2,…, не имеет нулей.

3°. Угол α такой, что предельное равенство

(1.1)

выполняется равномерно по

4°. Несобственный интеграл

(1.2)

сходится.

Тогда

(1.3)

где

Этот метод в дальнейшем назовем - метод.

Предложенный В.Д. Кулиевым - метод суммирования рядов, где , (см. глава) может служить весьма полезным инструментом исследования решений краевых задач. Чтобы показать аналитические преимущества 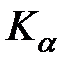-метода суммирования рядов, обратимся к известной задаче теплопроводности одномерного конечного стержня с заданным начальным распределением температур и граничными условиями на концах. Решение этой задачи записывается в виде ряда Фурье по собственным функциям соответствующей задачи Штурма-Лиувилля. Присутствие ряда затрудняет анализ и использование решения вне зависимости от формы записи, от того, включен ли ряд в функцию Грина или представлен в решении явным образом.

Секция: ПРОБЛЕМЫ, ВОЗМОЖНОСТИ И ПЕРСПЕКТИВЫ РАЗВИТИЯ МЕЖДУНАРОДНОГО БИЗНЕСА

Дата добавления: 2015-09-01