Линейные диофантовые уравнения

Важным приложением расширенного алгоритма Евклида являеться — "нахождение решения линейных диофантовых уравнений двух переменных", а именно, уравнения ax + by = c. Мы должны найти значения целых чисел для x и y, которые удовлетворяют этому уравнению. Этот тип уравнения либо не имеет решений, либо имеет бесконечное число решений. Пусть d = НОД (a, b). Если d†c, то уравнение не имеет решения. Если d|c, то мы имеем бесконечное число решений. Одно из них называется частным, остальные — общими.

Линейное диофантово уравнение — это уравнение двух переменных: ax + by = c.

Частное решение

Если d|c, то можно найти частное решение вышеупомянутого уравнения, используя следующие шаги.

1. Преобразуем уравнение к a₁x + b₁y = c₁, разделив обе части уравнения на d. Это возможно, потому, что d делит a, b, и c в соответствии с предположением.

2. Найти s и t в равенстве a₁s + b₁t = 1, используя расширенный алгоритм Евклида.

3. Частное решение может быть найдено:

Частное решение: X₀ = (c/d)s и y₀ = (c/d)t

Общие решения

После нахождения частного решения общие решения могут быть найдены:

Общие решения: x = x₀ + k(b/d) и y = y₀ – k(a/d), где k — целое число

22. Чтобы обеспечивать требуемые свойства современного блочного шифра, такие как рассеяние и перемешивание информации (обсуждается кратко), этот шифр формируется как комбинация модулей транспозиции (называемых P -блоками), модулей подстановки (называемых S -блоками) и некоторыми другими модулями (обсуждается кратко).

P -блок (блок перестановки) подобен традиционному шифру транспозиции символов. Он перемещает биты. В современных блочных шифрах мы можем найти три типа P -блоков: прямые P -блоки, P -блоки расширения и P -блоки сжатия.

Прямые P-блоки.Прямой P -блок с n входами и n выходами – это перестановка с n! возможными отображениями. P-блоки сжатия. P -блок сжатия – это P -блок с n входами и m выходами, где m <n. Некоторые из информационных входов блокированы и не связаны с выходом). P -блоки сжатия, используемые в современных блочных шифрах, обычно являются безключевыми с таблицей перестановки, которая указывает правила перестановки бит. Нам надо учитывать, что таблица перестановок для P -блока сжатия имеет m табличных входов, но в содержании каждого табличного входа – от 1 до n, и некоторые из них могут отсутствовать (те информационные входы, которые блокированы. P-блок расширения — P -блок с n входами и m выходами, где m> n. Некоторые из входов связаны больше чем с одним выходом. P -блоки расширения, используемые в современных блочных шифрах, обычно без ключа. Правила перестановки бит указываются в таблице. Таблица перестановки для P -блока расширения имеет m табличных входов, но m – n входов (те входы, которые связаны больше чем с одним информационным выходом). S-блок (блок подстановки) можно представить себе как миниатюрный шифр подстановки. Этот блок может иметь различное число входов и выходов. Другими словами, вход к S -блоку может быть n -битовым словом, а выход может быть m разрядным словом, где m и n — не обязательно одинаковые числа. Хотя S -блок может быть ключевым или без ключа, современные блочные шифры обычно используют S -блоки без ключей, где отображение от информационных входов к информационным выходам заранее определено.

S -блок — m x n модуль подстановки, где m и n не обязательно равны.

23. Асимметричное шифрование получило свое название из того факта, что в нем участвует два ключа. Один содержится в тайне (закрытый, или секретный, ключ пользователя), другой общедоступен (открытый, или публичный, ключ пользователя). Открытый ключ обычно помещается в общедоступные каталоги, и совершенно не имеет значения, кто будет иметь его копию.

Существует строгое математическое соответствие между закрытым и открытым ключами, которое заключается в том, что все, что зашифровано при помощи одного из двух ключей, может быть расшифровано только другим ключом пары. Длина ключей и вся математика, стоящая за ними, дают достаточную гарантию того, что не существует никакого другого ключа, не являющегося частью пары, который мог бы дешифровать сообщение.

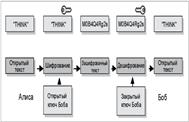
24. Цифровые подписи

Полезная вещь, которую дают нам алгоритмы асимметричного ключа.

Отправитель использует свой закрытый ключ для шифрования сообщения и затем отсылает его принимателю. Посланное сообщение хотя и является все еще зашифрованным, но больше уже не имеет частного характера, поскольку любой, у кого есть открытый ключ, может расшифровать его (все равно, у кого он есть).

Это сообщение от отправителя – авторизация. Поскольку только отправитель имеет доступ к закрытому ключу, при помощи которого было создано это сообщение, оно может прийти от него и только от него. В этом состоит понятие цифровой подписи.

Цифровые подписи участвуют в обеспечении целостности, аутентификации и идентификации, в определении авторства (невозможность отказа), в то время как алгоритмы и симметричного и асимметричного ключей.

9. Матрица — прямоугольный массив, содержащий l x m элементов, в которых l — число строк, m — число столбцов. Матрица обычно обозначается заглавной буквой, такой, как A. Элемент aij расположен в i -той строке и j -том столбце. Хотя элементы матрицы могут быть любым множеством чисел, мы обсуждаем только матрицы с элементами в Z. Пример матрицы с m столбцами и l строками

Если матрица имеет только одну строку (l = 1), она называется матрицей-строкой; если она имеет только один столбец (m = 1), то называется матрицей-столбцом. Матрица называется квадратной, если число строк равно числу столбцов (l = m) и содержит элементы a11, a22, ……, amm. Матрица обозначается 0, если все строки и все столбцы содержат нули. Единичная матрица обозначается I, если она квадратная и содержит все единицы на главной диагонали и все нули на других местах. Рисунок 3.2 показывает некоторые примеры матриц с элементами из Z.

Дата добавления: 2015-09-05