Определение вероятности безотказной работы

Используя несовместность событий "безотказная работа", "отказ по "0", "отказ по "1", можно записать

P + Q₀ + Q₁ = 1,

где P - вероятность безотказной работы ВО. Отсюда

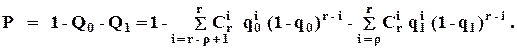(4.5)

При использовании ВО :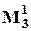

При использовании ВО :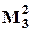

При использовании ВО :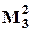

В заключение необходимо пояснить следующее. Для простоты везде опускался аргумент n. B действительности следует всегда помнить, что такая зависимость существует, т.е. правильнее писать

q₀(n), q₁(n), Q₀(n), Q₁(n), P(n).

Кроме того, предполагалась абсолютная надежность самого ВО.

Вопросы для самоконтроля

1. Структурная схема дискретного устройства с восстанавливающим органом, Пороговая функция восстанавливающего органа.

2. Перечислить и пояснить виды отказов, возникающих в дискретных устройствах. Раскрыть понятие модели логической неисправности.

3. Сколько и каких ошибок может исправить восстанавливающий орган .

4. Сколько и каких ошибок может исправить восстанавливающий орган .

5. Сколько и каких ошибок может исправить восстанавливающий орган .

6. Сколько и каких ошибок может исправить восстанавливающий орган .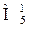

7. Показатели безотказности для систем с восстанавливающими органами.

5. ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ ДЛЯ АНАЛИЗА НАДЁЖНОСТИ СЛОЖНЫХ СИСТЕМ

5.1. Определение статистических значений показателей надежности систем по данным испытаний на надёжность и по статистическим данным о надёжности

Будучи важнейшей стороной эффективности применения, систем по назначению, надёжность должна как можно более полно и точно оцениваться. Лишь в редких случаях удается обойтись качественной оценкой надёжности, которая определяется, например, терминами: высокая, достаточная, низкая надёжность. В остальных ситуациях необходимыми являются количественные оценки надёжности, позволяющие принимать решения о мерах по повышению или поддержанию ее уровня в целях обеспечения достаточной эффективности системы, осуществлять количественно обоснованный выбор более совершенной из совокупности систем.

В этой связи вопросы количественного оценивания показателей надёжности находятся в центре внимания, как при разработке, так и в процессе эксплуатации систем. Решению этих вопросов в рамках теории надёжности придается важнейшее значение.

Наибольший объём информации о надёжности доставляют процессы различного рода испытаний, особенно испытаний на надёжность, а также процессы эксплуатации систем. Испытания на надёжность осуществляются в периоды экспериментальной отработки и производства. В зависимости от обстоятельств испытаниям подвергаются: элементная база, типовые блоки замены, конструктивно автономные части системы и система в целом. В интересах получения более точной и полной информации желательно, чтобы все выпускаемые образцы системы подвергались как можно большему числу видов испытаний в полном объеме. Однако это ведет к недопустимому удорожанию разработки и производства систем и не всегда практически возможно. Так, например, нельзя испытывать на функционирование средства разового использования. Поэтому проводятся только, крайне необходимые испытания на надёжность и им подвергается как можно меньшее число экземпляров технических объектов.

Проводятся следующие виды испытаний [1]: лабораторно-отработочные, конструкторско-доводочные, стендовые, с имитацией отказов и неисправностей, ресурсные, комплексные, на длительность хранения, специальные. Наряду с этим осуществляются натурные испытания (межведомственные, государственные) на образцах, передаваемых в серийное производство и эксплуатацию, в условиях, максимально близких к условиям реальной эксплуатации. Эти испытания дают наиболее полное представление о надёжности системы и ее элементов.

Испытания на надёжность могут быть определительными и контрольными. Определительные испытания проводят для оценки фактически достигнутого уровня надёжности. При этом во многих случаях предусматриваются ускоренные испытания на срок службы, а также испытания до разрушения.

Контрольные испытания проводят для определения соответствия фактического уровня надёжности заданному. Как правило, они реализуются путем совместной выборки наугад нескольких экземпляров системы из числа изготовленных или методом последовательных испытаний ряда экземпляров, выбираемых поочередно и в зависимости от предшествующих результатов.

Наряду с испытаниями большое значение для определения показателей надёжности имеют данные, которые выявляются в процессе эксплуатации. Они зависят от факторов, оказывающих влияние на функционирование систем в реальной обстановке. Существует возможность их получения для всех эксплуатируемых образцов системы. Наряду с этими неоспоримыми достоинствами данные о надёжности системы, полученные на стадии эксплуатации, обладают существенным недостатком: в условиях научно-технического прогресса они быстро устаревают и не в полной мере оказываются пригодными для систем нового поколения.

В силу вероятностного характера количественных показателей надёжности по данным испытаний и сведениям, полученным во время эксплуатации, можно определить такие показатели статистически. При этом используются различного рода модели, разработанные в теории надёжности на основе теории вероятностей и математической статистики.

Следует выделить два вида применяемых методов: аналитического и статистического моделирования. Аналитические методы включают зависимости для расчета показателей и зависимости для оценки соответствия этих показателей фактическим. Так как свойство надёжности носит вероятностный характер, то при построении расчетных зависимостей для оценки ее показателей предварительно выясняют следующие обстоятельства: известна ли форма закона распределения, известен ли его тип. Если форма закона распределения известна, то по испытаниям или данным эксплуатации достаточно определить его параметры (например, интенсивность отказов для экспоненциального распределения, математическое ожидание и среднее квадратическое отклонение времени безотказной работы для нормального распределения).

Если известен лишь тип закона распределения, то задача оценивания усложняется. В альтернативных случаях, когда о форме и типе закона распределения нет никакой информации, задача оценивания становится еще более сложной. В роли зависимостей для расчета показателей в простых случаях могут быть использованы выражения, рассмотренные в п. 1.3 для таких показателей, как выборочные (статистические) вероятность безотказной работы Р*(t), средняя наработка до отказа и интенсивность отказов l^*(t):

где N(t), N₀ - число объектов, не отказавших в течение времени t, и число

всех объектов, проходящих испытания;

t_i - период времени, по окончании которого i-й объект отказал;

Dt - приращение времени, обычно Dt «t.

В сложных случаях используются аналогичные детализированные в большей мере зависимости.

Зависимости для оценки соответствия рассчитываемых показателей надежности фактическим базируются на методах статистического оценивания. Эти методы позволяют ответить на вопросы, как рассчитать качественные оценки параметров надёжности по ограниченному объему (выборке) данных испытаний или эксплуатации, как определить достоверность таких оценок. Для расчета качественных оценок используется метод максимального правдоподобия, разработанной известным ученым Р. Фишером, и его частный случай - метод наименьших квадратов.

Качественной оценкой любого статистического показателя является несмещенная, эффективная и состоятельная оценка. Для несмещенной оценки ее математическое ожидание совпадает с истинным значением показателя. Эффективная оценка для данного объёма выборки имеет минимальную дисперсию. Состоятельность оценки определяется тем, что с увеличением объёма выборки оценка сходится по вероятности к истинному значению показателя. Достоверность оценок определяется с использованием понятия доверительного интервала, который определяется в зависимости от оценочного значения показателя и с достаточно высокой вероятностью покрывает неизвестное истинное значение того или иного параметра.

Охарактеризованные выше аналитические методы определения статистических значений показателей надёжности в ряде сложных случаев могут оказаться неприменимыми. Так, если случайная величина представляет сумму двух случайных величин, подчиненных различным законам распределения, то вопрос о законе ее распределения, а, следовательно, и о его параметрах, представляющих характеристики надёжности, зачастую не удается решить в рамках аналитического подхода, т.е. найти соответствующие суммарной случайной величине аналитические зависимости. В таких случаях полезным оказывается применение метода статистических испытаний, существо которого кратко излагается ниже.

5.2. Применение метода статистических испытаний для анализа надёжности сложных систем

Дата добавления: 2015-09-05