Структурные схемы восстанавливающих органов

Наиболее часто применяется случай, когда используются три идентичных логических блока. В этом случае r = 3 и можно реализовать три восстанавливающих органа: 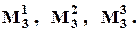Рассмотрим, какими функциями алгебры логики описываются указанные ВО, и каковыих корректирующие способности.

Восстанавливающий орган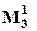

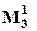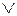Для этого ВО y = = y₁ y₂ 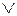y₃ (см. рис. 4.3, а). Он может корректировать г - r = 3 – 1 = 2 ошибки типа ложный " 0 ". Пусть, например, y₁ = 0, y₂ = 0. Тогда y 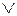= 0 0 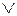y₃ = y₃ и ВО будет следовать за третьим исправным блоком. Корректировать же ложные " 1 " этот орган не может, так как в этом случае y = 1. Пусть, например, y₁ = 1. Тогда y = 1 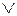y₂ 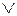y₃ = 1 и восстанавливающий орган перестает следовать за исправными блоками.

Восстанавливающий орган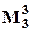

Для этого ВО y = 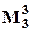= y₁y₂y₃ (см. рис. 4.3, г). Он может корректировать r - 1 = 3 - 1 = 2 ошибки типа ложная " 1 ". Пусть, например, y₁ = 1, y₂ = 1. Тогда y = 1 · 1 · y₃ = y₃ и ВО будет следовать за третьим исправным блоком. Корректировать же ложные " 0 " этот орган не может, так как в этом случае y = 0. Пусть, например, y₁ = 0. Тогда y = 0 · y₂ · y₃ = 0 и восстанавливающий орган перестает следовать за исправными блоками.

Восстанавливающий орган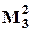

Для этого ВО возможны два варианта структурной схемы.

Вариант 1 (см. рис. 4.3, б). В этом случае y = y₁ · y₂ Ú y₁y₃ Ú y₂y₃.

Данный ВО корректирует r - 1 = 2 - 1 = 1 ошибку типа ложная "1" и

(r - r) = 3 - 2 = 1 ошибку типа ложный "0". Действительно, пусть, например, y₁ = 0, y₂ = 1. Тогда 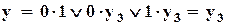и выход ВО будет следовать за третьим исправным блоком.

Если число ошибок типа ложный "0" на входе ВО равно или больше 2, то ВО тоже будет выдавать ошибочный сигнал. Пусть, например, y₁ = y₂ = 0. Тогда 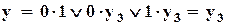. Такое же положение наблюдается, если имеются две или более ошибок типа ложная "1":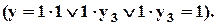

Вариант 2 (рис. 4.3, в). В этом случае

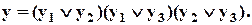
Аналогичной проверкой можно убедиться, что возможности этого варианта ВО такие же, как и у предыдущего.

Восстанавливающий орган 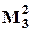широко распространен в сложных цифровых автоматизированных устройствах. Его чаще всего называют мажоритарным, а использование избыточности с таким ВО - мажоритированием.

4.3. Оценка надёжности дискретных устройств с ВО

4.3.1. Определение вероятности возникновения на выходе ВО отказа по "0"

Для дискретных устройств, как уже отмечалось, характерно два типа дефектов: устойчивый отказ и сбой. Рассмотрим оценку надежности дискретных устройств с ВО при устойчивых отказах.

Поставим вопрос: "В каких случаях может произойти отказ по "0" на выходе ВО"? Из предыдущего следует, что ВО корректирует не менее чем (r - r) ошибок типа ложный "0". Значит, если число ошибок будет равно (r - r + 1), (r - r + 2), …, r, то на выходе ВО будет постоянный нуль.

Рассмотрим теперь такой случай. Пусть известно, что по "0" отказали i блоков. Сколько всего возможно таких событий? Так как число блоков равно r, то, очевидно, искомое число событий равно 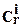, которое определяется по формуле

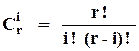(4.2)

и представляет собой число сочетаний из r по i. Все эти события будут несовместны.

Отсюда следует, что событие "отказ ВО" по "0" может произойти при реализации следующих элементарных событий:

- (г - r + 1) блоков отказали по "0", а остальные (r -1) не отказали по "0". Число таких событий будет равно 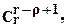а вероятность этой группы событий будет равна 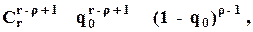где q₀ - вероятность отказа по "0" одного блока;

- (r - r + 2) блоков отказали по "0", а остальные (r - 2) блоков не отказали по "0". Число таких событий будет равно 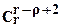, а вероятность этой группы событий будет равна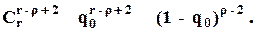

Аналогичные зависимости можно получить для остальных элементарных событий, когда отказали по "0" r - r + 3, …, r блоков.

Поскольку все элементарные события несовместны, то вероятность отказа по "0" определится следующим образом:

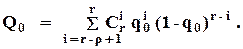(4.3)

При использовании ВО :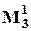

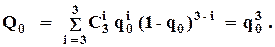
При использовании ВО :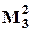

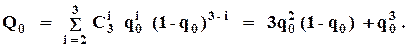
При использовании ВО :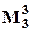

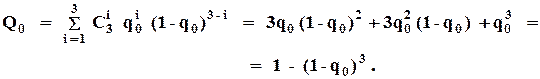
4.3.2. Определение вероятности возникновения на выходе ВО отказа по "1"

В этом случае отказ по "1" произойдет тогда, когда число ошибок типа ложная "1" будет равно r, r + 1, …, r.

Используя рассуждения предыдущего пункта, получим

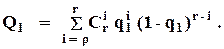(4.4)

При использовании ВО :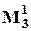

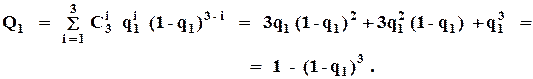
При использовании ВО :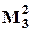

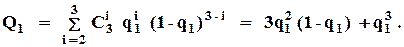
При использовании ВО :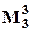

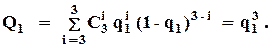
Дата добавления: 2015-09-05