Показатели ремонтопригодности

1. Вероятность восстановления работоспособного состояния – вероятность того, что время восстановления работоспособного состояния объекта не превысит заданного времени t (рис. 3.4):

, (3.9)

	Рис. 3.4

Функция представляет собой интегральную функцию распределения случайной величины . С вероятностной точки зрения она идентична рассмотренной ранее функции Q(t) (вероятности отказа) и имеет такие же свойства.

Статистически вероятность 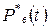определяется по формуле:

, (3.10)

где – число объектов, восстановленных за время t;

– число объектов, поставленных на восстановление.

2. Плотность вероятности восстановления работоспособного состояния объекта (частота восстановления, плотность (закон) распределения времени восстановления ) 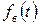– дифференциальная функция распределения случайной величины , определяется через производную от интегральной функции:

, (3.11)

где μ – интенсивность восстановления работоспособного состояния объекта.

Установим связь вероятности с характеристиками 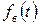и μ. Запишем уравнение (3.11) в виде и, после интегрирования обеих частей, получим:

,

. (3.12)

Вероятность является возрастающей экспонентой.

Статистическая оценка показателя :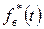

, (3.13)

где 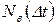– число объектов, восстановленных в интервале времени t.

3. Интенсивность восстановления объекта за время μ(t) – условная плотность вероятности восстановления объекта в момент времени t при условии, что до этого момента времени t восстановления объекта не произошло:

.

Для экспоненциального закона восстановления (3.12) характеристика μ(t) является постоянной μ(t) = μ в течении времени нормальной эксплуатации и ее точное значение равно:

, (3.14)

где – среднее время восстановления объекта.

Статистически интенсивность восстановления равна:

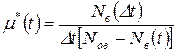, (3.15)

где – число не восстановленных объектов за время t.

4. Среднее время восстановления – математическое ожидание времени восстановления работоспособного состояния объекта (математическое ожидание случайной величины ).

Т.к. случайная величина является непрерывной, то

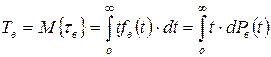. (3.16)

Приведем интеграл (3.16) к табличному виду , для чего введем следующие обозначения t = u, , , . После подстановки значений в (3.16), получим:

. (3.17)

В выражении (3.17) произведение при 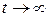будет равно единице, так как при 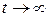вероятность будет стремиться к единице быстрее, чем параметр t будет стремиться к бесконечности и 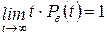. Подстановка нижнего предела t = 0 даст .

Таким образом, окончательно получим:

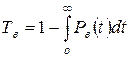. (3.18)

Определим связь между характеристиками Т_в и μ.

Для этого подставим в правую часть уравнения (3.17) значение вероятности и получим:

. (3.19)

Статистическая оценка показателя :

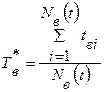, (3.20)

где – суммарное время, затраченное на восстановление всех возникших 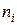отказов у i – го испытуемого объекта за время t;

– суммарное время восстановления всех 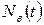образцов.

Учитывая, что для восстанавливаемых систем число восстановлений равно числу отказов, и каждый испытуемый объект за время испытаний может иметь несколько отказов, то характеристику (для удобства вычисления) можно определить по следующей формуле:

, (3.21)

где 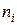– суммарное число отказов, возникших у i – го объекта за время испытаний t.

В формуле (3.21) верхнее значение N_в(t) в знаках суммирования можно заменить числом N_о, т.е. общим числом объектов, поставленных на испытание. В этом случае для не отказавших объектов соответствующие значения 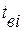и 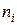будут равны 0. Тогда статистическая оценка будет иметь вид:

. (3.22)

Выражения (3.21) и (3.22) определяют характеристику как среднее время, затрачиваемое на восстановление одного отказа в одном объекте.

Дата добавления: 2015-09-05