Законы распределения наработки технического объекта до отказа и между отказами

Время t работы до первого отказа и время t⁰ между соседними отказами являются важнейшими характеристиками надёжности, точнее, безотказности невосстанавливаемых и восстанавливаемых технических объектов (ТО) соответственно. Так, если t⁰ для компьютера меньше времени решения какой-либо задачи, то результаты вычислений, скорее всего, либо не будут получены, либо окажутся неверными. Чем меньше t и t⁰, тем выше эксплуатационные затраты на устранение отказов и меньше длительность пребывания ТО в работоспособном состоянии. Более серьезные последствия могут быть при полете самолета, для которого t меньше, чем продолжительность рейса.

В соответствии с ГОСТ 27.002-89 "Надёжность в технике" характеристики t и t⁰ называются наработкой до отказа и наработкой между отказами.

Из опыта известно, что t и t⁰ следует рассматривать для большинства ТО как случайные величины. Охарактеризуем вначале t. Так как t - случайный промежуток времени от начала работы ТО до момента потери работоспособности, то наработка до первого отказа по своей физической природе является непрерывной величиной. Как известно, полная информация о непрерывной случайной величине содержится либо в законе (функции) распределения Q(t) случайной величины, либо в плотности вероятности случайной величины f(t). Функция Q(t) определяется как вероятность Р_t того, что t примет значение, не превосходящее времени t, при этом t не может быть отрицательным, т.е.

Q(t) = Pt { t £ t }, 0£ t £ (1.10)

Плотность f(t) представляет собой производную от Q(t).

Широкое применение в теории надёжности находит показательный, или, другими словами, экспоненциальный закон распределения. Строго говоря, он имеет место лишь в случаях, когда случайные события, представляющие отказы ТО, образуют так называемый простейший поток, т.е. такой процесс, который обладает свойствами ординарности, стационарности и отсутствием последействия. При этом наиболее простой аналитический вид Q(t) и другие вероятностные соотношения имеют в том случае, если в качестве основной характеристи­ки используется интенсивность отказов l(t). Как отмечалось,

(1.11)

где P(t) - вероятность того, что время t работы объектадо отказа будет больше t:

P(t) = Pt { t ≥ t } = 1 – Q(t). (1.12)

Из (1.12) видно, что функция P(t) несет столь же полную информацию о t, как и Q(t) или f(t). Она представляет собой вероятность безотказной работы ТО и очень часто используется в расчетах надежности. В этой связи Р(t) называется функцией надежности.

Для простейшего потока интенсивность отказов l(t) = const. На практике потоки отказов являются близкими к простейшим для многих современных ТО на определенных участках этапа эксплуатации.

Так как для периода нормальной эксплуатации l(t) = l = const для большинства рассматриваемых объектов, то имеет место экспоненциальный закон распределения случайной величины t. При этом

(1.13)

(1.14)

(1.15)

Эти зависимости могут быть получены различным образом. Наиболее просто они выводятся с использованием закона Пуассона

где F_k(t) - вероятность того, что в течение времени t произой­дет k отказов.

Найдем вероятность того, что в течение времени t не произойдет ни одного отказа ("наступит" 0 отказов).

поскольку (lt)⁰ и 0! равны 1. Вероятность F₀(t) является вероятностью того, что время до первого отказа не превосходит t, т.е. F₀(t) = P(t), откуда следует справедливость (1.15), а с учетом (1.12) - справедливость (1.13) и (1.14).

Эти же зависимости можно получить, используя (1.11). С учетом того, что

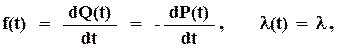
выражение (1.11) примет вид

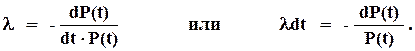
Интегрируя обе части полученного выражения на отрезке (0, t), получим

λt = - ln P(t).

После потенцирования этого выражения убедимся в справедливости (1.15).

Плотность распределения вероятности наработки до отказа представлена на рис.1.5.

Поскольку , то площадь под кривой f(t) равна 1, как для всякой плотности вероятности.

На практике большой интерес представляют такие показатели надёжности, как охарактеризованная в общем виде в п.1.3.4 средняя наработка до отказа, представляющая согласно ГОСТ 27.002-89 ''Надежность в технике" математическое ожидание T₀ случайной величины t, а также ее дисперсия D_t или среднее квадратичное отклонение σ_t, . Показатель Т₀ характеризует t в среднем, является характеристикой положения t на оси времени, а s_t характеризует рассеивание, разброс значений t относительно Т₀. В соответствии с зависимостью (1.8) найдем, что для экспоненциального закона

Заменим - lt = x, тогда при t = 0, x = 0, а при t=¥, х = - ¥;

(1.16)

Следовательно, Т₀ является величиной обратной l. Для определения s_t используем известное выражение для дисперсии и (1.14). В результате получим, что

Интеграл под корнем берется по частям и равен откуда

(1.17)

То обстоятельство, что при экспоненциальном распределении величины t показатели Т₀ и s_t совпадают, используется как подтверждение его справедливости, если полученные статистическим путем аналоги Т₀ и s_t оказываются близкими по величине.

Отметим, что в приближенных расчетах используются зависимости

Q(t) ≈ λt, P(t) ≈ 1 – λt, (1.18)

которые получаются после разложения 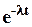в ряд Тейлора до линейного члена. При этом, если lt 0,1, ошибка в определении значений Q(t) и Р(t) не превышает 5%. Впрочем, для функции e^-x составлены подробные таблицы (см., например, [1]), на большинстве компьютеров она вычисляется как встроенная.

Таким образом, если имеет место экспоненциальный закон распределения вероятностей наработки до первого отказа t, то достаточно определить один из показателей l, Т₀, s_t, чтобы рассчитать Q(t), P(t), f(t) для любых t. В этом смысле экспоненциальный закон является однопараметрическим, так как полностью определяется одним параметром, например интенсивностью отказов l.

Можно показать, что если отказы ТО образуют простейший поток, то в связи с отсутствием последействия наработка между отказами t⁰ характеризуется точно так же, как и t. В частности,

При этом t⁰ = [ t_i, t_i + 1 ], где t_i - момент возникновения i-го отказа ТО, i = 1,2,...; [ t_i, t_i + 1 ] промежуток времени между i-м и (i + 1)-м отказами.

В периоды приработки и износа, а также для некоторых ТО в период нормальной эксплуатации показательный закон для t, t⁰ может оказаться неприемлемым. Наиболее распространенным в этих случаях законом распределения является нормальный. В первую очередь это относится к периоду износа и старения, для которого характерны постепенные отказы.

Как известно, при нормальном распределении случайная величина может принимать любые значения от -¥ до +¥. Пос­кольку временные случайные величины не могут иметь отрицательных значений, для них может быть использован лишь усеченный нормальный закон.

Усеченным нормальным распределением случайной величины называется распределение, получаемое из нормального при ограничении интервала возможных значений этой величины. Так как возможные значения случайной величины t ограничены положительными значениями, то плотность вероятностей для усеченного распределения

q(t) = c f(t),

где:

f(t) - плотность не усеченного распределения

, (1.19)

(Т₀ = a, s_t = s обозначено для краткости записи);

С - нормирующий множитель, определяемый из условия

то есть

Так как нормальное распределение применяется обычно для описания отказов, возникающих вследствие износа и старения, то средняя наработка до отказа a имеет большую величину и a >> s.

В этом случае с большой степенью точности, поэтому С = 1 и, следовательно, можно пользоваться формулой обычного нормального распределения (1.19).

Определять значения q(t) при заданных t, а и s можно используя таблицы, построенные для плотности вероятностей так называемой нормированной центрированной случайной величины с а = 0 и s = 1. Такая плотность имеет вид

Действительно, сравнивая q(t) и f₀(t), получим

(1.20)

Полезно знать, что f₀(-t) = f₀(t), ввиду симметрии кривой f₀(t) относительно оси ординат.

Функция распределения для нормального закона определяется следующим образом:

(1.21)

Как известно, интеграл в формуле (1.21) не выражается через элементарные функции, поэтому для его вычисления пользуются таблицами специальной функции, которая называется нормированной функцией Лапласа:

(1.22)

Для этого упростим (1.20), применив следующие подстановки:

Получим

Таблицы для Ф(Z) имеют только положительные значения Z. Как быть в том случае, если t < а, и < 0? Для этого покажем, что Ф(-Z) = = 1 – Ф(Z). Действительно,

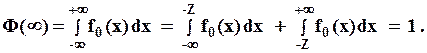
Ввиду симметрии f₀(x)

Тогда получаем Ф(-Z) + Ф(Z) = 1, откуда Ф(-Z) = 1 - Ф(Z).

Теперь легко записать характеристики надёжности при нормальном распределении случайной величины t в прежних обозначениях.

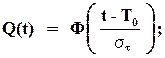
Зависимости основных показателей надёжности при нормальном распределении t представлены на рис. 1.6.

Как видно, закон нормального распределения t - двухпараметрический. Его параметрами являются средняя наработка Т₀ до отказа (математическое ожидание случайной величины t) и среднее квадратичное отклонение s_t .. Аналогичным образом в периоды приработки, износа и старения может быть распределена вероятность случайной величины t⁰, представляющая наработку между отказами.

Рис. 1.6.

На практике экспоненциальное и нормальное распределения t и t⁰ наиболее распространены. Для ряда ТО оказывается необходимым применение других распределений.

Вопросы для самоконтроля

1. В чем сущность проблемы надежности в военном деле?

2. Что такое объект, система, элемент системы?

3. Как Вы понимаете термин надёжность?

4. Какие Вы знаете свойства надёжности?

5. Какие этапы жизненного цикла, эксплуатационные процессы Вы знаете?

6. Каковы состояния технического объекта в процессе эксплуатации Вы знаете?

7. Как можно определить понятия повреждение, отказ, дефект?

8. Какова классификация отказов сложных технических систем?

9. Дайте статистическое и вероятностное определение вероятности безотказной работы.

10. Дайте статистическое и вероятностное определение вероятности отказа.

11. Дайте статистическое и вероятностное определение интенсивности отказов.

12. Дайте статистическое и вероятностное определение средней наработки до отказа.

13. Дайте статистическое и вероятностное определение плотность распределения отказов.

14. Какие основные законы распределения времени работы до отказа: виды, сущность, соотношения Вы знаете?

Дата добавления: 2015-09-05