Определение показателей надежности при постоянном общем резервировании

Будем полагать, что отказы элементов системы являются независимыми событиями и что изменение нагрузки не влияет на надежность.

Определение показателей надежности при постоянном общем резервировании (см. рис. 2.5). Пусть P₀(t), P₁(t),..., P_m(t) - вероятности безотказной работы, Q₀(t), Q₁(t),..., Q_m(t) - вероятности отказа основного и m резервных элементов, P_C(t) и Q_C(t) - вероятности безотказной работы и отказа системы, образовавшейся в результате общего резервирования основного элементавсеми резервными.

По условию отказ наступает в тот момент, когда выходит из строя последняяиз работающих подсистем. Следовательно, отказ системы является произведением (m + 1) независимых событий, поэтому

Q_C(t) = Q₀(t) × Q₁(t) ×... × Q_m(t).

Так как Р_C(t) = 1 - Q_C(t) и Р_i(t) = 1 – Q_i(t),

то P_C(t) = 1 - .

Для равнонадёжных элементов

Q_C(t) = [Q₀(t)]^m+1, P_C(t) = 1 – [1 – P₀(t)]^m+1. (2.7)

При показательном законе надёжности в этом случае

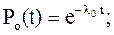
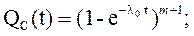
(2.8)

где - интенсивность отказов любой из m+1 систем.

При l₀t «1

Q_C(t) ≈ (l₀t)^m+1; P_C(t) ≈ 1 - (l₀t)^m+1. (2.9)

Найдем выражение для средней наработки до отказа.

Очевидно,

.

Обозначим , тогда и

. (2.10)

Вычислим плотность вероятности и интенсивность отказов системы:

(2.11)

(2.12)

Таким образом, при показательном законе распределения наработки до отказа равнонадёжных основного и резервных объектов в случае постоянного общего резервирования наработка до отказа системы как случайная величина характеризуется функцией распределения и законом надежности в виде (2.8), (2,9), плотностью вероятности в виде (2.11) и показателями надежности Т_С и l_c(t) в виде (2.10) и (2.12).

Дата добавления: 2015-09-05