Вероятностное определение. Как всякая непрерывная случайная величина,t имеет математическое ожидание

Как всякая непрерывная случайная величина, t имеет математическое ожидание, которое называется в данном случае средней наработкой до отказа

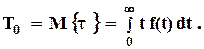
Полезно преобразовать этот интеграл к другому виду, взяв его по частям:

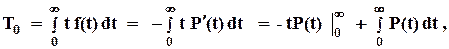
или

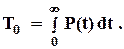(1.8)

В выражении t · P(t) при t → ∞ P(t) → 0 быстрее, чем t → ∞, в результате чего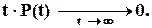

Средняя наработка до отказа является удобным и распространенным показателем надёжности. Однако, как всякая числовая характеристика случайной величины, Т₀ не имеет полной информации о ней и в этом смысле не эквивалентна таким показателям, как Р(t), f(t), l (t).

Дата добавления: 2015-09-05