Читайте также:
|
Для статистического определения функций Р(t) и Q(t), как впрочем, и других показателей надёжности, используются данные о следующем опыте по испытанию объектов. Испытанию подвергаются N0 образцов. В процессе испытаний фиксируется наработка каждого образца до отказа t1, t2,..., tN0. По этим значениям определяется функция N(t) - число образцов, не отказавших к моменту времени t. Тогда статистически вероятность безотказной работы может быть определена как отношение числа безотказно работающих образцов в момент времени t к общему числу образцов, поставленных на испытание,
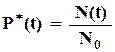. (1.3)
Показатели надёжности Р(t), Q(t) используются для характеристики, как простейших элементов, так и сложных систем и даже комплексов.
Дата добавления: 2015-09-05; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вероятностное определение | | | Вероятностное определение |