Автоматизированное управление гидроманипуляторами

Манипулятор служит для наведения захватывающего рабо­чего органа и пильного аппарата на дерево, его перемещения и укладки. На рис. 12.4 представлена принципиальная гидрокине­матическая схема манипулятора. Принцип работы основан на отрабатывании механической системой задаваемого положения в пространстве. Задаваемое положение производится одной масштабной рукояткой, которая находится в кабине оператора.

Применение такой гидравлической следящей системы позволяет производить управление только одной масштабной рукояткой сразу всеми конструктивными элементами механической си­стемы, состоящей из стойки 1 с захватами, гидроцилиндров 3, золотников 7, рукоятки 2 и стрелы 4.

Масштабная рукоятка кинематически аналогична механиче­ской системе. Она состоит из рычага 1' имитирующего стойку 1. рычагов 2' и 4' имитирующих рукоять 2 и стрелу 4.

Работа такой гидравлической следящей системы происходит следующим образом. При повороте масштабной рукоятки, на­пример 4' на угол a₁, рычаги 5 переместят шток золотника 6 на величину Х_Ш, вследствие чего поршни золотника смещаются относительно своего нейтрального положения (по отношению

к корпусу 7), открывая проходное сечение. Масло по трубо­проводу поступает в штоковую полость гидроцилиндра 3 управ­ления стрелой 4. Шток гидроцилиндра, воздействуя на стрелу, начинает ее перемещать в сторону заданного положения ры­чагом 4' масштабной рукоятки. При повороте стрелы поворачи­вается ее рычаг обратной связи 8, который перемещает корпус золотника 7 относительно его поршней. Это движение будет происходить до тех пор, пока поршни золотника не перекроют отверстие трубопровода, идущего к цилиндру 3 стрелы 5, т. е. угол a₂ = a₁.

Таким образом отрабатывается задаваемое положение в про­странстве стрелой 4. Аналогичным образом одновременно по

времени отрабатываются положения рукояти 2 стойки 1 меха­нической системы, так как рычаги 2' и 1' масштабной рукоятки в процессе перемещения поворачивают свои рычаги 5 (на ри­сунке не показаны), которые воздействуют соответствующим об­разом на штоки и корпус своего золотника.

Для определения устойчивости данной следящей системы со­ставим ее блок-схему. Для упрощения решения задачи рас­смотрим сначала следующую систему только для одной стрелы 4 (рис. 12.5).

На схеме имеем P₁ —рычаги 5 (см. рис. 12.4) привода штока золотника; ГЗ — гидроцилиндр с золотником; С — стрела 4; Р₂ — рычаг обратной связи 8; a₁ — угол поворота рычага мас­штабной рукоятки 4'; Х ₁ — перемещение штока золотника Х_шт; Χ ₃ — перемещение корпуса золотника Х_кор; Δ f = f _шт— f _кор— пло­щадь проходного сечения при смещении штока золотника, f _кор — площадь проходного сечения при смещении корпуса золотника; Х₂ — перемещение штока гидроцилиндра; a ₂ — угол поворота стрелы 4.

Составим уравнения звеньев системы и их передаточные функции.

При повороте рукоятки 4' на угол α₁ перемещение штока зо­лотника составит X ₁ =k ₁ a ₁. Это уравнение пропорционального звена, передаточная функция которого будет W ₁(P)=k ₁, где k ₁ определяется из соотношения плеч рычагов 5 (см. рис. 12.4).

Относительное изменение площади проходного сечения

Тогда передаточная функция сравнивающего устройства бу­дет

Передаточная функция гидроцилиндра с золотником опреде­ляется выражением

Коэффициент усиления k₃ определяется как

а постоянная времени Τ с учетом массы подвижной системы определяется как T = mtga, где т — приведенная масса по­движной системы; а — угол наклона, определяемый по механи­ческой характеристике гидроцилиндра (рис. 12.5,б).

Изменение угла поворота стрелы 4 (см. рис. 12.4) гидро­манипулятора, очевидно, будет

Тогда передаточная функция этого пропорционального звена будет

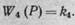
Уравнение перемещения корпуса золотника X ₃ = k ₅ a ₂, а его передаточная функция

Уравнение разомкнутой следящей системы определяется как

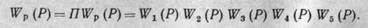
А уравнение замкнутой системы с отрицательной обратной связью определяется как

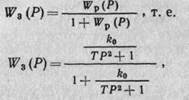
где k₀ = k₁k₂k₃k₄k₅

Из теории автоматического регулирования известно, что следящие системы, описываемые уравнениями второго по­рядка, устойчивы при любых значениях постоянных величин вышенаписанных уравнений элементов.

Теперь рассмотрим устойчивость конкретной автоматиче­ской системы (рис. 12.5, в) в динамической взаимосвязи между стрелой 4 и рукоятки 2 (см. рис. 12.4). Как видно из рисунка, движения стрелы и рукояти взаимосвязаны, так как при их неравномерном движении масса стрелы воздействует на ру­коять со стойкой 1 и наоборот. С этой точки зрения возникает вопрос об устойчивости такой взаимосвязанной следящей си­стемы.

На рис. 12.5,в эта взаимосвязь между стрелой С и руко­ятью со стойкой P ₁ показаны стрелками. Точка А' изображает положение масштабной рукояти, т. е. ее пространственное по­ложение задается оператором, а точка А отрабатывает это задаваемое положение механической системой манипулятора.

Дифференциальное уравнение перемещающейся в прост­ранстве стрелы 4 (см. рис. 12.4) будет

где I _a2 —момент инерции стрелы с учетом массы рукояти со стойкой; ξ — коэффициент вязкого трения; М_с — момент сухого трения; Μ — момент относительно В, создаваемой весом стрелы и рукояти со стойкой; P ₁ — рабочее давление жидкости в гид­роцилиндре привода стрелы или рукояти; D — диаметры цилин­дров стрелы или рукояти; l_{a 2} — плечо приложенного усилия от штока гидроцилиндра.

Аналогичное дифференциальное уравнение и для рукояти 2 со стойкой 1 (см. рис. 12.4) в зависимости от угла β₂.

Значением М_C и М, как это увидим, можно пренебречь, тогда будем иметь

Заметим, что перемещения стрелы и рукояти определяются углами их поворота, т. е. α₂ и β₂·

Тогда скорость перемещения стрелы определится как

, а рукояти

, таким образом рабо­чее давление в гидроцилиндрах представляет собой некоторые функции от α₂ до β₂, точнее от Δα ₁ α ₂ и Δβ, β₂ ( где Δα = α ₁ —α₂; Δβ = βι-β₂).

Учитывая это, уравнение движения стрелы и рукояти во взаимосвязи можно представить в общем функциональном виде:

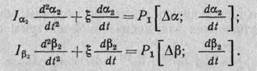
Значения рабочего давления Р ₁ в функции от Δα,

приведены на рис. 12.6. С учетом этих зависимостей и разло­жения этой функциональной зависимости в ряд Тейлора с огра-

ничениями членов разложения до первого порядка получим следующие уравнения:

Здесь А _α и B_β — значения числа, которые могут быть заданы большими заранее заданного, так как они являются танген­сами углов наклона касательных к кривым, показанным на рис. 12.6.

Преобразовав эти уравнения, запишем их в операторной форме:

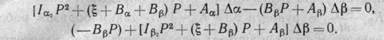
Определители этих характеристик уравнений, записанные в матричной форме, будут

Раскрывая определитель и скобки, получим общее характе­ристическое уравнение взаимосвязанной системы стрелы и ру­кояти:

коэффициенты характеристического уравнения будут

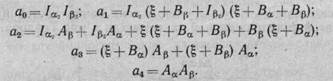
Полученное характеристическое уравнение и коэффициенты используются для решения задачи об устойчивости взаимосвя­занной системы.

Дата добавления: 2015-08-27