Промышленными роботами

При выполнении операций с помощью манипулятора {рис. 11.3), когда одно из звеньев поворачивается на больший угол, чем другие, и движется с большей скоростью, возникают пики ускорений на захвате. Поэтому необходимо снизить ско­рости линейного и вращательного движений. Наиболее сильно влияние сказывается на участке пуска (рис. 11.4). Так как ус­корение пуска определяется углом вращения φ, угловой ско­ростью ω, ускорением ω и его изменением, то следует задавать законы изменения этих величин и обеспечить их выполнение ап-паратурно.

Для определения оптимального времени позиционирования вектора а ускорения, действующего на захват, можно разло­жить на три составляющих"· нормаль а_п, бинормаль пь и каса­тельную a_t в системе координат, связанной с захватом (см. рис. 11.3). В декартовой системе координат эти векторы совпа­дут с осями координат. В случае произвольной системы коор­динат вектор пространственной траектории перемещения за­хвата из точки Ро(фо, т)о, То) в точку Ρι (φι, ηι, τι) имеет вид

Векторы скорости

и ускорения

являются соответственно первой и второй производной вектора г.

Выражая вектор ускорения а через компоненты векторов

в той же системе координат, получим:

где

ρ, z, τ — составляющие вектора в цилин­дрической системе координат. Таким образом, если заданы

значения функций φ(t),η(t),τ(t),το можно найти ускорения (за­медления) в период разгона (торможения). Выражения функ­ций φ(t), η(t), τ(t) можно определить из тахограммы движения (см. рис. 11.4). Так как

то разбив интервал 0 — t на три периода: разгон, установив­шееся движение и торможение (включая доводку на «ползучей» скорости) и заменив интегралы суммами, запишем выражение

Значения пределов суммирования вычисляются из выражения для угла перемещения захвата

Тогда, решая интегральное выражение (11.3), получим

Из выражения (11.6) определяется время установившегося движения:

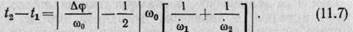
Тогда при (t₂ — t₁)≥0

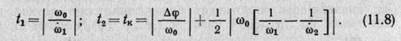
Такой расчет времени потребуется для управления движе­нием каждого звена. Уравнение (11.3) позволяет определить скорость ω₀, если известны характер функции ω(t) и прираще­ние скорости

Скорости остальных звеньев могут быть найдены из квадра­тичных уравнений

Аналогично рассчитывают значения

и

Таким образом, снизить влияние ускорений на захвате можно, изменяя параметры контуров регулирования. Для пози-ционно-скоростного управления используется метод ограниче­ния скорости, который хотя и не позволяет полностью компен­сировать влияние ускорений, но вполне приемлем. Основные вычисления сводятся к решению линейных уравнений вида (11.10) и (11.11).

Применение позиционно-скоростного управления позволяет выполнить сложные операции, требующие управления положе-

Рис. 11.5. Структурные схемы устройства управления промышленным роботом

нием рукояти робота и ориентацией захвата с высокой точ­ностью. Рассмотрим структурную схему управления роботом (рис. 11.5,а). Значение выходной величины, определяющее пе­реходный процесс в системе Х(Р):

где К(Р) —передаточная функция системы; К⁰_xf (Р) — переда­точная функция, определяющая связь выходной величины X с возмущением f; K_Uf(P), Κ_xU(Ρ) —передаточные функции компенсационного воздействия по /. В дифференциальной форме выражение (11.13) будет иметь вид

где D(P) —многочлен вида

М(Р) —соответствует первому слагаемому выражения (11.13);

M_К(P) —второму слагаемому. Изображение по Лапласу вы­ходной величины Х(Р):

где М_Н(P) —многочлен, определяемый ненулевыми начальными условиями (М_Н(Р)= — Р²I, здесь I — изменяющийся в широких пределах обобщенный момент инерции; F(P), G(P) — изобра­жения по Лапласу соответственно для возмущения и входного задающего воздействия; D(P) =P² + Pk_v+k_п, тогда

Подавление влияния внешних возмущений при одновремен­ном сохранении желаемого соотношения вход-выход может быть осуществлено с помощью замкнутой комбинированной САУ с каналами обратной связи (рис. 11.5,б) по положению k_n и по скорости k_v. В этой схеме для формирования реакции от­клика обратной связи при разгоне и компенсации инерционного запаздывания введено дифференцирующее звено Р, а отрица­тельная обратная связь позволяет уменьшить инерционность, улучшить устойчивость и подавить колебания. Уравнение, оп­ределяющее переходный процесс в системе при торможении, бу­дет иметь вид

Из уравнения (11.17) видно, что реакция системы сущест­венно зависит от меняющегося момента инерции /, поэтому для компенсации этого влияния в схему необходимо добавлять до­полнительную обратную связь — канал / (рис. 11.5,в), тогда

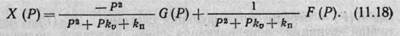
При этом условие критического торможения

показывает, что реакция системы уже не зависит от конфигу­рации рукояти робота. Для компенсации отклонений сигнала задания G(P) в схему (см. рис. 11.5, в) введено звено Р², а для исключения влияния силы тяжести груза добавлено воздействие F_Д/P, равное по модулю и противоположное по знаку этой силе. Аппаратурная реализация компенсации возмущений и обрат­ных связей дает хорошие результаты позиционно-скоростного управления лесным роботом. Понятно, что для роботов миниа-

тюрных изделий требуется микронная точность позиционирова­ния по прецизионным операциям. В этом случае выполняется адаптивный подход к организации САУ ПР с использованием идентификатора в цепи обратной связи.

Дата добавления: 2015-08-27