Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Синтез математической модели управления по таблице состояния

ТИПОВЫЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ОБЪЕКТАМИ | ИЛ. ОБЩИЕ ХАРАКТЕРИСТИКИ СИСТЕМ ЧИСЛОВОГО ПРОГРАММНОГО УПРАВЛЕНИЯ (ЧПУ) | КЛАВИШНАЯ СИСТЕМА ЧПУ ОБРЕЗНОГО СТАНКА | СИСТЕМЫ ЧПУ СТАНОЧНОГО ОБОРУДОВАНИЯ НА БАЗЕ МИКРОЭВМ | ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ РОБОТОТЕХНИКИ | СРЕДСТВА ОЧУВСТВЛЕНИЯ ПРОМЫШЛЕННЫХ РОБОТОВ | ПРОМЫШЛЕННЫМИ РОБОТАМИ | АППАРАТНЫЕ СРЕДСТВА СИСТЕМ УПРАВЛЕНИЯ ПРОМЫШЛЕННЫМИ РОБОТАМИ | УСТРОЙСТВА УПРАВЛЕНИЯ РОБОТАМИ НА БАЗЕ ПРОГРАММИРУЕМЫХ ЛОГИЧЕСКИХ МАТРИЦ | УСТРОЙСТВА УПРАВЛЕНИЯ ПРОМЫШЛЕННЫМИ РОБОТАМИ НА БАЗЕ МИКРОКОНТРОЛЛЕРОВ |


Читайте также:
  1. BPwin и система просмотра модели
  2. Cookies и хранение состояния
  3. ERwinимеет два уровня представления модели - логическийи физический. Логический
  4. Model Explorer - навигатор модели
  5. PR как функция управления коммуникациями
  6. Автоматизированных систем управления промышленным предприятием
  7. АВТОМАТИЧЕСКАЯ ИДЕНТИФИКАЦИЯ МОДЕЛЕЙ ОБЪЕКТОВ УПРАВЛЕНИЯ

Для однотактных систем наиболее просто и эффективно со­ставлять таблицы состояния, по которым синтезируется мате­матическая модель управления объектом.

В ранее рассмотренном примере (см. рис. 10.1) управле­ния электролампой рассматривали следующую таблицу состоя­ний (табл. 10.1).

Таблица 10.1

№ п/п x 1 x 2 у № п/п x 1 x 2 у
               
               

Очевидно, что условие включения лампы у будет опреде­ляться законом единицы (y =1), т. е. условие включения дан­ной цепи управления будет иметь вид

где f' (2,4)—условия включения второй и четвертой (2, 4) строки.

Из таблицы видно, что f'2 = x 1 x 2 а f' 4 = x 2 x 1.

Подставив, получим у = x 1 x 2 + x 2 x1, pанее известную нам ма­тематическую модель управления объектом не по словесной модели, а по таблице состояний.

В общем случае условия включения составляются по за­кону единицы или по закону нуля. Условие включения по за­кону единицы есть выражение вида f 1 '=Πχi — произведение хi в данной строке. Условие включения по закону нуля есть выра­жение вида f" i = (Пxi) = Σxi — отрицание произведения условий включения есть сумма инверсий xi (см. правила преобразо­вания).

Учитывая это, можно составить математическую модель включения по закону единицы — y 1=Σf' = Σ Пxі - сумма произве­дений xi, или по закону нуля у0 = (Σ f ") = (Пf") = Π Σ xi —произве­дения сумм xi.

Обращаясь к нашей таблице состояний управления элек­тролампой, будем иметь

x 1 x 2 f 2 ' — вторая строка условия включения; x 2 x 1 = f 4 ' —четвер­тая строка условия включения.

Преобразуем это выражение (откроем скобки)

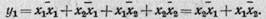
Если же мы условие включения составим по закону нуля, то будем иметь

где (x 1+ x 2) = f 1 " — первая строка условия выключения; (x 1 + + x 2 ) = f 3" — третья строка условия выключения. Преобразуем выражение

Выражение x 1 x 1=0 и x 2 x 2=0, тогда окончательно будем иметь

т. е. мы лишний раз показали, что условия включения системы можно выразить по законам нуля или единицы. Выбор этого

закона определяется количеством единиц и нулей в колонке таблицы состояний, которых меньше, по ним для простоты и производятся построения математической модели управления системой.

Дата добавления: 2015-08-27; просмотров: 65 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
МАТЕМАТИЧЕСКИЕ МОДЕЛИ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ОБЪЕКТАМИ| СИНТЕЗ МАТЕМАТИЧЕСКОЙ МОДЕЛИ УПРАВЛЕНИЯ ПО ЦИКЛОГРАММЕ
mybiblioteka.su - 2015-2024 год. (0.007 сек.)