Читайте также:
|
Определим напряжения, возникающие в ненагруженном стержне вследствие неравномерного прогрева его сечения, когда температура изменяется по координатам x и y и не изменяется по z (рис. 7.1).
Напряжение в произвольной точке сечения определяется по формуле (7.5):
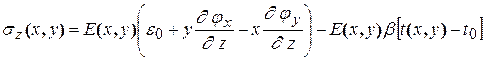. (7.26)
Параметры деформации определим из условий равновесия отсеченной (правой) части стержня в отсутствии внешних нагрузок:
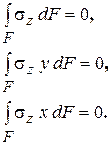(7.27)
Подстановкой σ z = σ ( x, y ) образуем систему уравнений:
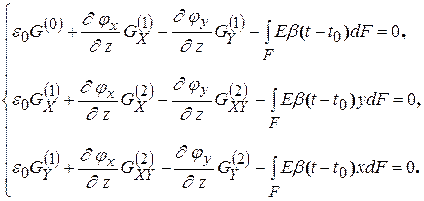(7.27)
Используя свойства главных центральных осей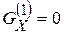 
, 
, 
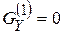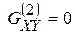, найдем параметры деформации:
, 
, 
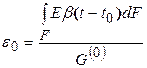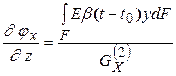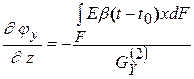. (7.28)
Зная их, определим распределение температурных напряжений (7.26):
| (7.29) |
.
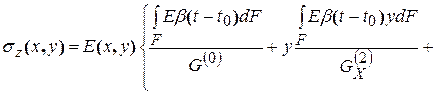
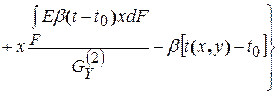В двигателестроительных конструкторских бюро России и Украины эта формула используется для расчетов температурных напряжений в лопатках турбин и известна как формула Биргера — Малинина.
Если температуры в сечении стержня таковы, что изменением модуля упругости и коэффициента теплового расширения можно пренебречь, то из нее следует более простая зависимость:
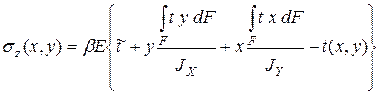, (7.30)
где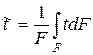 
— средняя температура сечения.
Дата добавления: 2015-08-26; просмотров: 93 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Изгиб при неравномерном нагреве | | | ОПТИМИЗАЦИЯ СИСТЕМЫ ОХЛАЖДЕНИЯ ЛОПАТКИ |