Гипотеза плоских сечений

Первое важнейшее допущение, используемое при расчетах распределения напряжений по стержневой теории, — знаменитая гипотеза плоских сечений Бернулли — Эйлера. Гипотеза предполагает, что деформация стержня происходит таким образом, что точки плоского поперечного сечения остаются в одной плоскости. Исследования показывают, что гипотеза подтверждается, когда касательные напряжения малы по сравнению с нормальными напряжениями. Это условие выполняется на расстояниях от торца стержня и точки приложения силы, больших размера сечения.

Перемещение вдоль оси Z точки поперечного сечения с координатами x, y по гипотезе плоских сечений можно представить как результат параллельного перемещения сечения вдоль Z и его поворота вокруг X и Y (см. рис. 7.1). Считая углы поворота малыми, получим

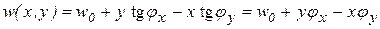, (7.1)

где w ₀ — перемещение точки 0; φ_x, φ_y — углы поворота сечения вокруг осей X и Y. Величины w ₀, φ_x, φ_y одинаковы для всех точек сечения, но изменяются по оси Z.

Деформация в направлении оси Z определяется по формуле

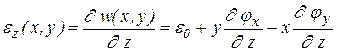, (7.2)

где ε_{ 0} = ¶ w ₀ ¤ ¶ z — деформация на оси стержня. Таким образом, гипотезе плоских сечений соответствует линейное распределение деформации ε_z по плоскости поперечного сечения.

Второе допущение — гипотеза о ненадавливании, предполагающая отсутствие нормальных напряжений σ_x и σ_y в площадках, перпендикулярных осям X и Y. Ее строгое обоснование исходит из того, что боковая поверхность стержня свободна от напряжений, а производная напряжения по нормали к боковой поверхности ограничена. Если размеры поперечного сечения незначительны по сравнению с длиной стержня, то напряжения σ_x и σ_y незначительны по сравнению с σ_z.

В области упругости материала справедлива суперпозиция деформаций, связанных с нормальными напряжениями, и температурной деформации, вызванной нагревом:

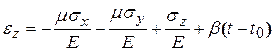. (7.3)

Используя гипотезу о ненадавливании σ_x = σ_y = 0, получим

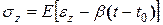. (7.4)

Принимая также и гипотезу плоских сечений, будем иметь

. (7.5)

Таким образом, для расчета распределения напряжений по сечению

σ_z = σ_z (x, y) должны быть определены параметры ε ₀, ¶φ_x ¤ ¶z, ¶φ_y ¤ ¶z и известны распределения: температуры t = t (x,y), модуля упругости E=E (x,y) и коэффициента линейного расширения β=β (x,y).

Дата добавления: 2015-08-26