Читайте также:
|
При определении напряжений в неравномерно нагретых деталях используются так называемые упругогеометрические характеристики сечений, которые учитывают непостоянство модуля упругости по сечению. Эти характеристики далее будем называть термоупругими жесткостями.
Будут использоваться следующие характеристики:
— термоупругая жесткость нулевого порядка (при растяжении):
, (7.6)
где x и y — координаты в сечении F, dF – элементарная площадка;
— термоупругие жесткости первого порядка относительно осей X и Y (статические жесткости):
, (7.7)
; (7.8)
— термоупругие жесткости второго порядка относительно осей X и Y (жесткости при изгибе):
, (7.9)
; (7.10)
— двухосевая термоупругая жесткость второго порядка:
. (7.11)
Из приведенных выше определений видно, что порядок термоупругой жесткости равен сумме степеней при координатах в подынтегральных выражениях.
Если ось X удовлетворяет условию 
, то она является центральной осью термоупругой жесткости. В плоском сечении существует бесчисленное множество центральных осей. Все они пересекаются в одной точке - центре термоупругой жесткости сечения.
Из определений (7.9), (7.10) следует, что термоупругая жесткость второго порядка относительно любой оси всегда положительна. Оси X и Y, удовлетворяющие условию 
, называют главными осями термоупругой жесткости. В плоском сечении всегда существуют только две главные оси (исключение составляют симметричные сечения, у которых может быть бесконечное множество главных осей). Обе они перпендикулярны друг другу, являются одновременно центральными осями и, следовательно, проходят через центр термоупругой жесткости.
При постоянном модуле упругости из выражений (7.6) – (7.11) следует:
Рисунок 7.2-Смещение
центра жесткости при локальном нагреве участка ΔF
|
;
; 
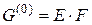; (7.12)
; 
; 
,
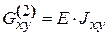где 
- площадь сечения; 
и 
— статические моменты сечения относительно осей X и Y; 
и 
— осевые моменты инерции относительно осей X и Y;
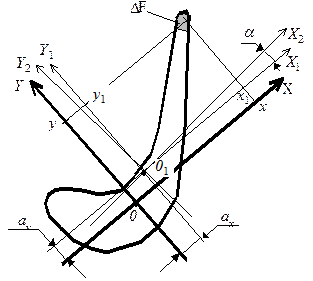 Рисунок 7.3-Смещение и поворот главных осей термоупругой жесткости при локальном нагреве
|
— центробежный момент инерции относительно системы координат X и Y.
Величины F, Sx, Sy, Jx, Jy, Jxy являются геометрическими характеристиками сечения, так как определяются только конфигурацией сечения. В отличие от них упругогеометрические характеристики зависят еще и от распределения модуля упругости по сечению.
Неравномерное распределение температур в сечении приводит к смещению центра термоупругой жесткости относительно центра тяжести сечения, а также к смещению и повороту главных осей термоупругой жесткости относительно главных осей инерции.
Центр термоупругой жесткости удаляется от области уменьшения модуля упругости (нагрева). Это проиллюстрировано движением точки а на рис. 7.2. В случае увеличения модуля, наоборот, приближается к участку нагрева.
Поворот главных осей жесткости при локальном уменьшении модуля упругости происходит таким образом, что ось максимальной жесткости приближается к участку сечения, в котором произошло изменение (ось Х2 на рис.7.3). При увеличении модуля упругости ось максимальной жесткости удаляется от участка изменения.
Дата добавления: 2015-08-26; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Гипотеза плоских сечений | | | Растяжение при неравномерном нагреве |