Растяжение при неравномерном нагреве

Рассмотрим случай, когда на стержень действует сила Р, растягивающая его вдоль продольной оси Z. Для упрощения выкладок будем использовать систему координат, оси которой X и Y являются главными осями поперечного сечения стержня, а ось Z проходит через центр термоупругой жесткости — точку 0 (см. рис. 7.1).

Первоначально основное внимание уделим распределению силовых напряжений. Для этого исключим из формулы (7.5) температурные напряжения, приняв β = 0:

. (7.13)

Для определения параметров деформации, входящих в это уравнение, воспользуемся условиями равновесия отсеченной (правой) части стержня. Приравнивая равнодействующие внутренних сил и моментов внешним силам и моментам, получим

(7.14)

Подстановкой значения σ_z в выражение (7.13), образуем систему уравнений:

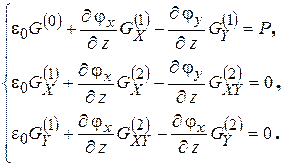(7.15)

Используя свойства главных центральных осей 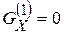, , 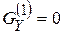, 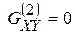найдем три параметра деформации:

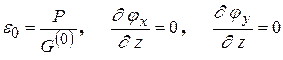. (7.16)

Знание их позволяет определить по формуле (7.13) силовое напряжение в любой точке сечения стержня:

. (7.17)

Вводя среднее по сечению значение модуля упругости , получим

. (7.18)

В равномерно прогретом стержне значение модуля упругости постоянно, , и напряжения в сечении не зависят от его величины. Напряжения будут постоянными, равными изоупругому значению: σ_и = P/F. Если сечение прогрето неравномерно, то напряжения будут отличаться от этого значения. В "горячих" частях сечения, как правило, 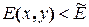и напряжения меньше изоупругого значения. В “холодных” частях, наоборот, и напряжения будут больше. Эта закономерность проиллюстрирована на рис. 7.4.

Отличие механических напряжений от изоупругого значения может быть значительным. Например, для сплавов на никелевой основе, применяемых для изготовления лопаток авиационных турбин, при изменении температуры по сечению от 700°С до 1000°С отношение изменяется в пределах , то есть отличие напряжений может достигать ±20%, что существенно, учитывая небольшие запасы прочности, используемые при проектировании деталей авиационных турбин.

Формулы (7.17), (7.18) указывают на еще одну важную закономерность. Распределение напряжений зависит не столько от величины модуля упругости, сколько от ее изменения в пределах сечения. При одинаковом (в k раз) изменении модуля упругости во всех точках сечения напряжения не изменяются.

Равенство нулю производных в решении (7.16) означает отсутствие поворотов поперечных сечений по всей длине стержня: j_x =0 и j_y =0, то есть при растяжении (сжатии) стержня силой, действующей по линии, проходящей через центры жесткости поперечных сечений, деформирование происходит без поворота сечений.

Примечание. Причиной рассмотренного здесь изменения напряжений по сечению является переменность модуля упругости. Другая причина (возникновение температурных напряжений) пока не учитывалась. Они исключены принятием допущения β = 0 в формуле (7.13).

Дата добавления: 2015-08-26