Изгиб при неравномерном нагреве

Рассмотрим действие на неравномерно нагретый стержень моментов M_X и M_Y относительно главных осей его поперечного сечения X и Y. Силовые напряжения будем определять по формуле (7.5) при β = 0:

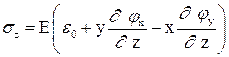. (7.19)

Используем условия равновесия отсеченной (правой) части стержня в отсутствии растягивающей силы (см. рис. 7.1):

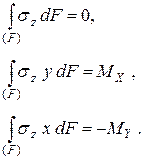
Подстановкой σ_z из формулы (7.19) образуем систему уравнений:

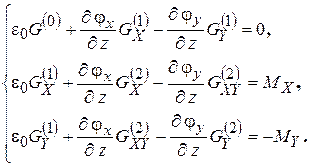(7.20)

Используя свойства главных (центральных) осей 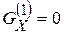, , 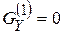, 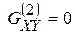определим параметры деформации:

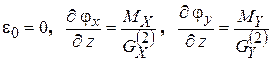, (7.21)

что дает возможность определять напряжения исходя из формулы (7.19):

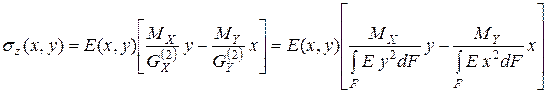. (7.22)

Если значение модуля упругости постоянно E ( x, y ) = E =const, то напряжение линейно зависит от координат и не зависит от модуля упругости:

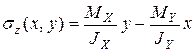. (7.23)

Такое значение напряжения будем называть изоупругим значением при изгибе. По сути, оно состоит из напряжения 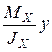, связанного с действием момента М_Х, определяющего распределение напряжений вдоль оси Y, и напряжения 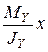, связанного с действием момента М_Y, определяющего распределение напряжений вдоль оси X.

Если ввести средние осевые значения модуля упругост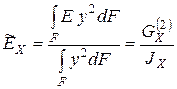и

и 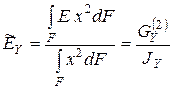, (7.24)

то распределение напряжений (7.23) заменится формулой

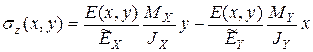. (7.25)

Таким образом, при изгибе влияние зависимости модуля упругости от температуры можно учесть коррекцией слагаемых изоупругого значения (7.23) коэффициентами, равными отношению местного значения модуля упругости к соответствующему среднему осевому значению. В "горячих" частях сечения, как правило, 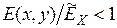и 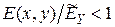. Следовательно, напряжения будут меньше изоупругого значения (7.23). В "холодных" частях, наоборот, 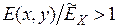, 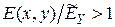и напряжения превышают изоупругое значение.

Рисунок 7.5- Силовые напряжения при изгибе: а — схема нагружения; б — примеры распределения температур; в — эпюры напряжений

Эта закономерность распределения напряжений проиллюстрирована на рис. 7.5 для симметричного и линейного распределений температуры при изгибе относительно одной оси Х (М_Х >0, M_Y = 0).

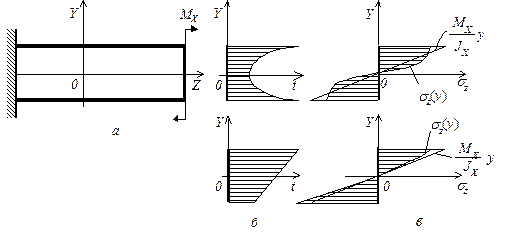Изоупругие значения, рассчитанные по формуле (7.23), можно использовать как первоначальную оценку напряжений на этапе предварительного расчета, когда распределение температуры еще неизвестно. С помощью формулы (7.25) они легко могут быть скорректированы по ожидаемым значениям отношений модулей упругости. После определения температурного поля можно провести окончательный расчет распределения напряжений по формуле (7.25), учтя также изменение положения главных осей (7.24) при неравномерном нагреве.

Дата добавления: 2015-08-26