Интерпретация решения ДУ, проверка его достоверности

Общий интеграл ДУ задает семейство интегральных линий, которые имеют уравнение

.

- это семейство окружностей с центром в точке (C;0) и радиусом |C|, где C – произвольно изменяющаяся величина, постоянная относительно переменных x и y.

y

А₂

Проверим правдоподобность решения задачи при С=1

геометрически подтверждается, что для нескольких точек окружности условие задачи выполняется так как .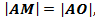

A 8 -идачедачи удовлетворяютений для чек окружности енных орые называется общим интегралом ДУ порядка относительно функции ₁

M₁

М₂

x

M

A

Замечаем, что при C=0 окружность превращается в точку , следовательно, поставленная задача не имеет решения.

Если проанализировать теорему существования и единственности частных решений для ДУ 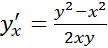, то хорошо видны его особые точки – это такие точки, в которых или . Следовательно, составленная математическая модель задачи не дает решение для точек с или .

Ответ по задаче:

Условию задачи удовлетворяют окружности , в которых

.

Дата добавления: 2015-08-26