
|
Читайте также: |
Определите тип дифференциального уравнения, найдите его общее решение и
найдите частное решение, если поставлены начальные условия:
1.1. 
1.2. 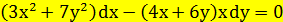 ;
;
1. 3. 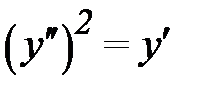 ,
,  ,
, 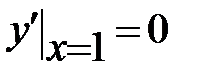 ;
;
1.4.  ;
;
1.5.  ;
;
1.6.  .
.
Решение
1.1. 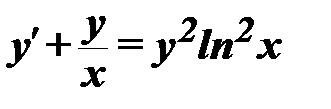 ,
, 
Данное ДУ первого порядка относительно функции  имеет вид обобщённого линейного уравнения (уравнения Бернулли):
имеет вид обобщённого линейного уравнения (уравнения Бернулли):
 , в котором
, в котором  ,
,  ,
,  .
.
В соответствии с теоретическим методом решения, следует искомую функцию  искать в виде произведения двух функций
искать в виде произведения двух функций  и
и  , для каждой из которых всегда получается дифференциальное уравнение с разделяющимися переменными:
, для каждой из которых всегда получается дифференциальное уравнение с разделяющимися переменными:
 =>
=>  ;
;
ДУ:  <=>
<=>  <=>
<=>
 ;
;
ДУ для 
 <=>
<=>  <=>
<=>  <=>
<=> 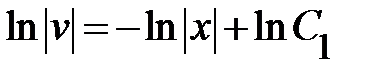 <=>
<=> 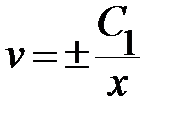 <=>
<=> 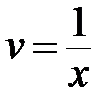 ;
;
в проведённых выкладках заменялось  на
на  , где
, где  , а затем фиксировалось
, а затем фиксировалось  , что допустимо в решении линейных ДУ первого порядка;
, что допустимо в решении линейных ДУ первого порядка;
ДУ для 
 <=>
<=>  <=>
<=>  <=>
<=>
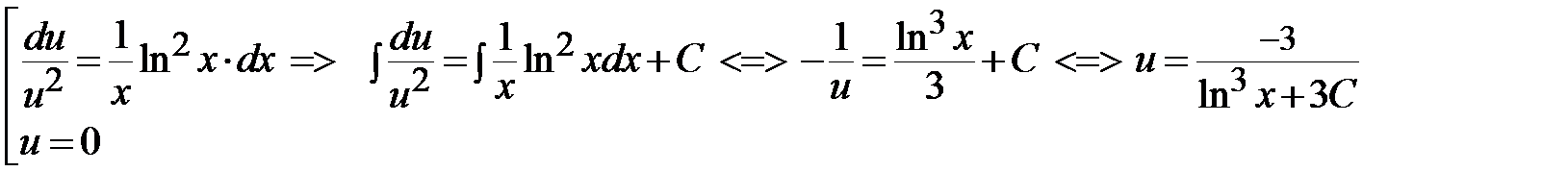
<=>  или
или  (сделано переобозначение
(сделано переобозначение  на
на  ).
).
Перемножением функций  и
и  находим общее решение данного ДУ
находим общее решение данного ДУ  .
.
Если рассмотреть случай  , то получим функцию
, то получим функцию  , которая удовлетворяет исходному дифференциальному уравнению, но является его особым решением, так как ни при каком значении постоянной
, которая удовлетворяет исходному дифференциальному уравнению, но является его особым решением, так как ни при каком значении постоянной  эта функция не получается из найденного общего решения.
эта функция не получается из найденного общего решения.
Решаем задачу Коши:
так как имеем начальное условие  , то подставляем
, то подставляем  и
и  в общее решение и находим значение произвольной постоянной
в общее решение и находим значение произвольной постоянной  , при котором будет удовлетворяться это начальное условие:
, при котором будет удовлетворяться это начальное условие:
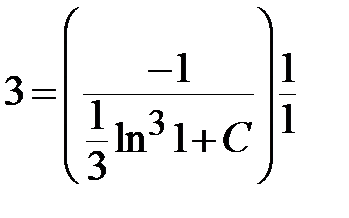 < =>
< => 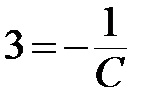 <=>
<=>  ;
;
возвращая это значение  в решение, получаем искомое частное решение:
в решение, получаем искомое частное решение:
 <=>
<=> 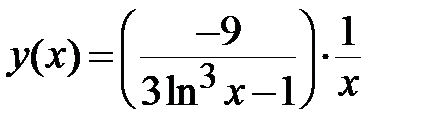 .
.
Заметим, что особое решение 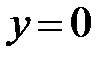 не удовлетворяет поставленному начальному условию, поэтому получаем только одну интегральную линию, проходящую на плоскости
не удовлетворяет поставленному начальному условию, поэтому получаем только одну интегральную линию, проходящую на плоскости  через точку
через точку  .
.
Ответ по задаче 1.1: 1)  - общее решение,
- общее решение,
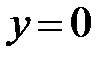 - особое решение данного ДУ;
- особое решение данного ДУ;
2) 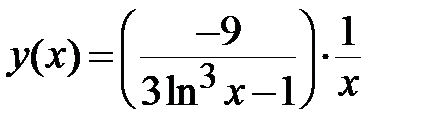 - искомое частное решение.
- искомое частное решение.
1.2 
Преобразуем данное ДУ к каноническому виду ДУ первого порядка, чтобы определить его тип:
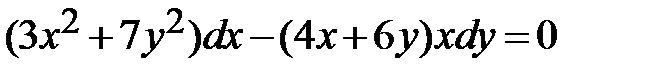 <=>
<=> 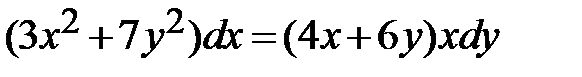 =>
=>
 <=>
<=>  - однородное ДУ первого порядка, так как имеет вид
- однородное ДУ первого порядка, так как имеет вид  .
.
Теоретический метод решения: заменить  , тогда
, тогда 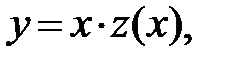
 .
.
Выполняем эту замену в ДУ и получаем ДУ с разделяющимися переменными относительно функции 
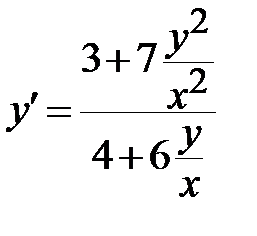 <=>
<=>  <=>
<=>  <=>
<=> 
<=> 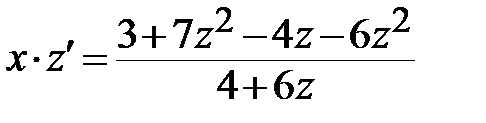 <=>
<=> 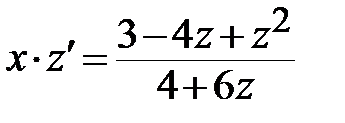 <=>
<=>  <=>
<=>
 ВЫДЕЛИТЬ ПЕРЕХОД
ВЫДЕЛИТЬ ПЕРЕХОД
вычисление интеграла, стоящего в левой части равенства:
 =
=  =
=
 ;
;
<=> 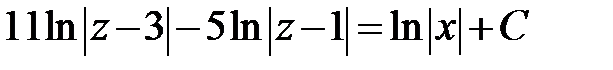 - это общий интеграл ДУ относительно функции
- это общий интеграл ДУ относительно функции 
Выполняем обратную замену, подставив в общий интеграл 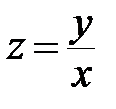 :
:
 <=>
<=>  ;
;
Нахождение общего решения  из последнего равенства затруднительно, поэтому для ответа ограничимся общим интегралом, но преобразуем его к более простому виду без логарифмов:
из последнего равенства затруднительно, поэтому для ответа ограничимся общим интегралом, но преобразуем его к более простому виду без логарифмов:
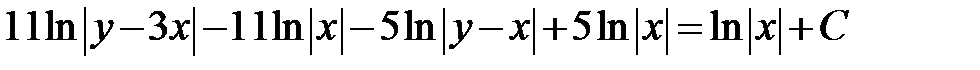 <=>
<=>  , где
, где 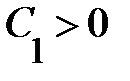 <=>
<=>  <=>
<=>
 <=>
<=>  ,
,  , где
, где  .
.
Дополнительно разберёмся с равенством 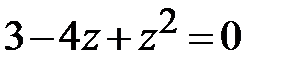 , которое может дать особое решение исходного ДУ:
, которое может дать особое решение исходного ДУ:
 ;
;
чтобы проверить, являются ли эти функции решениями исходного ДУ, их следует подставить в первоначальное равенство «до делений»:
 <=>
<=>
 - верно при любых x =>
- верно при любых x =>
функция 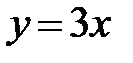 удовлетворяет исходному дифференциальному уравнению, следовательно, является его решением; сопоставив это решение с общим интегралом данного ДУ, видим, что оно получается из общего интеграла при значении
удовлетворяет исходному дифференциальному уравнению, следовательно, является его решением; сопоставив это решение с общим интегралом данного ДУ, видим, что оно получается из общего интеграла при значении  ; поэтому функция
; поэтому функция  особым решением не является, но в общий интеграл следует подключить значение
особым решением не является, но в общий интеграл следует подключить значение  .
.
Аналогично функцию  подставим в исходное ДУ «до делений»:
подставим в исходное ДУ «до делений»:
 <=>
<=>
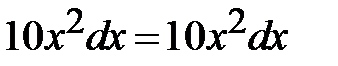 - верно при любых x =>
- верно при любых x =>
функция  также является решением исходного ДУ; но эта функция не получается из общего интеграла ни при каком числовом значении произвольной постоянной
также является решением исходного ДУ; но эта функция не получается из общего интеграла ни при каком числовом значении произвольной постоянной  ; поэтому функцию
; поэтому функцию  следует записать в ответ как особое решение.
следует записать в ответ как особое решение.
Ответ по задаче 1.2: 
1.3.  ,
,  ,
, 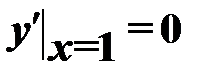
Имеем ДУ второго порядка относительно функции  , которое относится к типу ДУ, допускающих понижение порядка, так как не содержит в явном виде аргумент
, которое относится к типу ДУ, допускающих понижение порядка, так как не содержит в явном виде аргумент  (теоретический вид дифференциальных уравнений этого типа:
(теоретический вид дифференциальных уравнений этого типа:  ). В соответствии с теоретическим методом решения выполняем следующую замену:
). В соответствии с теоретическим методом решения выполняем следующую замену: 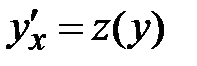 =>
=> 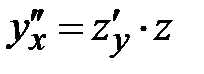 .
.
 <=>
<=> 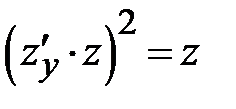 <=>
<=> 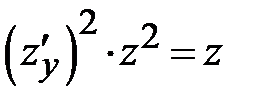 <=>
<=> 
 <=>
<=> 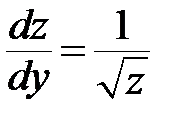 <=>
<=>  <=>
<=>  <=>
<=>  <=>
<=>  =>
=>  .
.
Так как  то получено, что
то получено, что  <=>
<=>  - ДУ I порядка с разделяющимися переменными относительно функции
- ДУ I порядка с разделяющимися переменными относительно функции 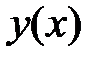
=> 
=>  <=>
<=>  <=>
<=>
 <=>
<=>  =>
=>  ;
;
переобозначим произвольные постоянные  и
и  , включив в них постоянные множители:
, включив в них постоянные множители:  и
и 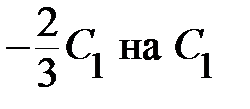 ; в результате получим общее решение исходного ДУ в следующем виде:
; в результате получим общее решение исходного ДУ в следующем виде:  .
.
Функция  , которая дважды получалась в процессе решения, удовлетворяет исходному ДУ и является его особым решением, так как не получается из общего решения ни при каких значениях постоянных
, которая дважды получалась в процессе решения, удовлетворяет исходному ДУ и является его особым решением, так как не получается из общего решения ни при каких значениях постоянных 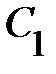 и
и  .
.
Решаем задачу Коши:
 ,
, 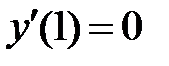 - эти начальные условия подставляем в общее решение и в его производную:
- эти начальные условия подставляем в общее решение и в его производную:
 <=>
<=>  ;
;
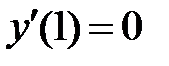 =>
=>  =>
=>  ;
;
 =>
=>  =>
=> 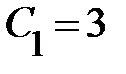 ;
;
подставляем найденные значения  и
и  в общее решение и получаем искомое частное решение:
в общее решение и получаем искомое частное решение:  .
.
Заметим, что поставленным начальным условием можно удовлетворить и особым решением: если  , то
, то  и
и 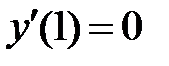 ; тогда получаем и особое частное решение
; тогда получаем и особое частное решение  .
.
Таким образом, через заданную точку 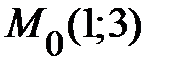 проходят две интегральные линии данного дифференциального уравнения второго порядка.
проходят две интегральные линии данного дифференциального уравнения второго порядка.
Ответ по задаче 1.3: 1)  - общее решение,
- общее решение,
 - особое решение данного ДУ;
- особое решение данного ДУ;
2)  и
и  - искомые частные решения.
- искомые частные решения.
1.4. 
Имеем дифференциальное уравнение второго порядка относительно функции y (x); его тип определяем как линейное неоднородное ДУ с постоянными коэффициентами, так как структура данного ДУ согласуется с канонической формой 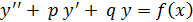 , в которой p, q – числа,
, в которой p, q – числа,  .
.
На основании теоремы об общем решении дифференциального уравнения указанного типа, обще решение данного ДУ ищем в виде 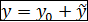 ,
,
где  – это общее решение соответствующего однородного ДУ,
– это общее решение соответствующего однородного ДУ,
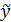 – какое-нибудь частное решение данного неоднородного ДУ.
– какое-нибудь частное решение данного неоднородного ДУ.
Найдем  :
:  - соответствующее линейное однородное дифференциальное уравнение (ЛОДУ); на основании теоремы об общем решении линейного однородного ДУ имеем
- соответствующее линейное однородное дифференциальное уравнение (ЛОДУ); на основании теоремы об общем решении линейного однородного ДУ имеем  ,
,
где  и
и  - произвольные постоянные,
- произвольные постоянные,  и
и  - фундаментальная система частных решений (ФСЧР).
- фундаментальная система частных решений (ФСЧР).
ФСЧР для ЛОДУ с постоянными коэффициентами находится с помощью характеристического уравнения:
 <=>
<=>  - корни действительные различные => ФСЧР:
- корни действительные различные => ФСЧР:  =>
=>  .
.
Найдём 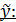 сначала анализируем правую часть исходного линейного неоднородного дифференциального уравнения (ЛНДУ) с целью установить имеет ли она специальный вид:
сначала анализируем правую часть исходного линейного неоднородного дифференциального уравнения (ЛНДУ) с целью установить имеет ли она специальный вид:  – подходит под первый специальный вид
– подходит под первый специальный вид  , в котором
, в котором  ,
,  .
.
В соответствии с теоретической рекомендацией, частное решение ЛНДУ с такой
правой частью ищем в следующем виде: 
 . Неопределённые коэффициенты A и B находим из условия, что
. Неопределённые коэффициенты A и B находим из условия, что 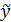 удовлетворяет исходному ЛНДУ:
удовлетворяет исходному ЛНДУ:

так как 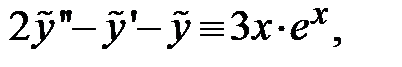 то
то  <=>
<=>  <=>
<=> 
таким образом получено, что  .
.
Выполним проверку найденного частного решения:

 - верно.
- верно.
Общее решение исходного ЛНДУ находим суммированием 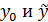 :
:
 .
.
Решаем задачу Коши:

подставляя поочерёдно начальные условия в общее решение и его производную, получаем систему уравнений для определения значений постоянных  и
и  :
:









возвращаем числовые значения  и
и  в общее решение и получаем искомое частное решение, то есть такое частное решение, которое соответствует поставленным начальным условиям:
в общее решение и получаем искомое частное решение, то есть такое частное решение, которое соответствует поставленным начальным условиям:
 .
.
Ответ по задаче 1.4: 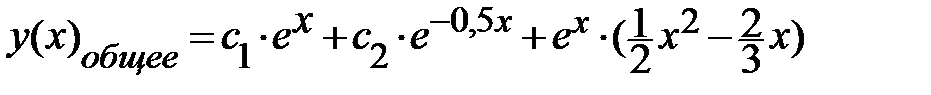 ;
;
 .
.
1.5 
Имеем линейное неоднородное ДУ с постоянными коэффициентами и правой частью, вид которой не является специальным.
Теоретический метод решения:  , где
, где  - общее решение соответствующего однородного ДУ,
- общее решение соответствующего однородного ДУ, 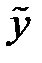 - какое-нибудь частное решение данного неоднородного ДУ.
- какое-нибудь частное решение данного неоднородного ДУ.
Найдем  :
:  - ЛОДУ с постоянными коэффициентами =>
- ЛОДУ с постоянными коэффициентами =>  , где
, где  ,
,  - ФСЧР,
- ФСЧР,  ,
, 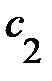 - произвольные постоянные;
- произвольные постоянные;
ФСЧР составляем по корням характеристического уравнения:
 <=>
<=>  - случай равных действительных корней =>
- случай равных действительных корней =>
ФСЧР:  ,
,  =>
=> 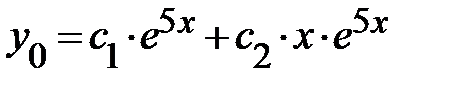 .
.
Найдём  методом вариации произвольных постоянных, так как правая часть данного ЛНДУ не имеет специальный вид; суть этого метода состоит в том, что функцию
методом вариации произвольных постоянных, так как правая часть данного ЛНДУ не имеет специальный вид; суть этого метода состоит в том, что функцию  берём в таком же виде, в котором получилась функция
берём в таком же виде, в котором получилась функция  , но произвольные постоянные
, но произвольные постоянные  и
и 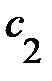 заменяем на функции от x:
заменяем на функции от x:
 ;
;
в соответствии с теоретической разработкой этого метода, производные функций  и
и  следует определять из следующей системы функциональных уравнений:
следует определять из следующей системы функциональных уравнений:  , в которой
, в которой 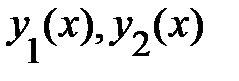 - ФСЧР соответствующего ЛОДУ,
- ФСЧР соответствующего ЛОДУ,  - правая часть данного ЛНДУ;
- правая часть данного ЛНДУ;
составляем эту систему для данного ДУ, упрощаем её и находим её решения, используя формулы Крамера:
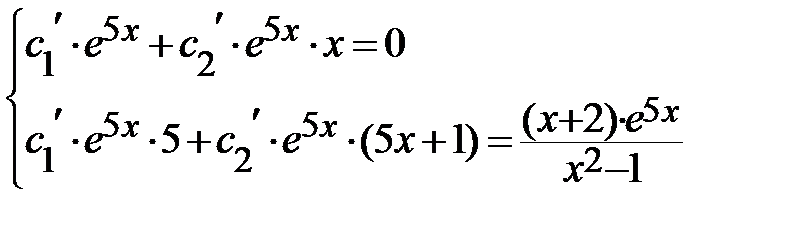 <=>
<=>  =>
=>
 => система имеет единственное решение,
=> система имеет единственное решение,
 ,
,  =>
=>
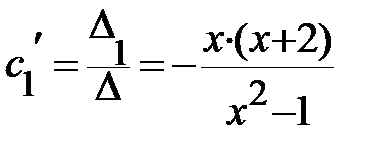 ,
,  - это и есть решение системы, которое всегда следует подтвердить проверкой;
- это и есть решение системы, которое всегда следует подтвердить проверкой;
функции  и
и  восстанавливаем по их найденным производным с помощью неопределённого интеграла:
восстанавливаем по их найденным производным с помощью неопределённого интеграла:

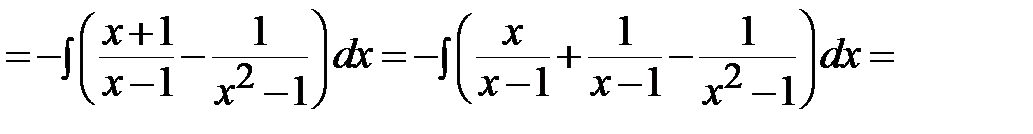


 , где
, где  - постоянная интегрирования;
- постоянная интегрирования;


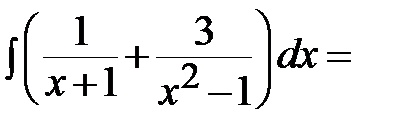

 , где
, где  - постоянная интегрирования;
- постоянная интегрирования;
найденные функции  и
и  подставляем в формулу для
подставляем в формулу для  и получаем:
и получаем:
 ;
;
так как 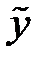 - это какое-нибудь частное решение ЛНДУ, то константами интегрирования
- это какое-нибудь частное решение ЛНДУ, то константами интегрирования  и
и 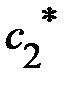 можно распорядиться удобным образом, например, положить их равными нулю; в результате функция
можно распорядиться удобным образом, например, положить их равными нулю; в результате функция  упростится к следующему виду:
упростится к следующему виду:
 .
.
Общее решение исходного ЛНДУ находим суммированием функций  и
и 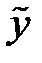 и дальнейшими упрощениями полученного выражения.
и дальнейшими упрощениями полученного выражения.
Ответ по задаче 1.5:
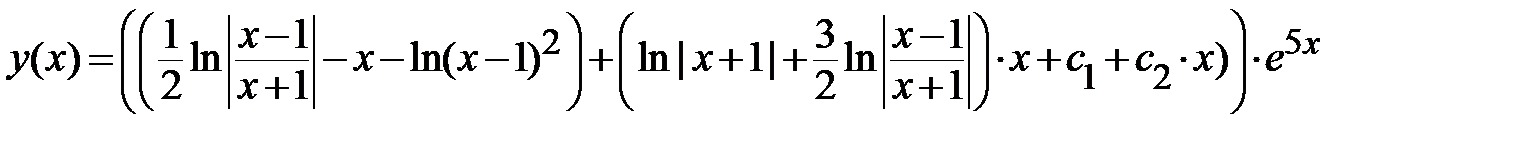 .
.
1.6. 
Данное дифференциальное уравнение второго порядка имеет тип линейного неоднородного ДУ (ЛНДУ) с постоянными коэффициентами. Уравнение такого типа уже встречалось в выполняемом задании, поэтому можно его каноническую форму не приводить и суть метода решения подробно не описывать.
Ниже приводится краткое решение этого ДУ:
1)  , где
, где  - общее решение собственного ЛОДУ,
- общее решение собственного ЛОДУ,
 - какое-нибудь частное решение
- какое-нибудь частное решение
данного ЛНДУ;
2) находим 
 =>
=>  , где
, где
 - это ФСЧР,
- это ФСЧР,
 - произвольные постоянные;
- произвольные постоянные;
характеристическое уравнение:
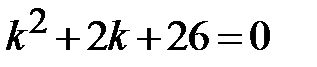 <=>
<=>  - комплексно-сопряжённые корни;
- комплексно-сопряжённые корни;
=> ФСЧР:  ,
, 
=>  ;
;
3) находим 
анализируем правую часть исходного ЛНДУ:
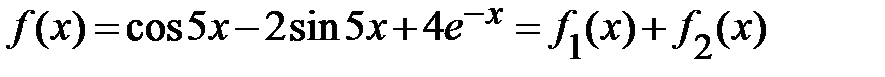 , где
, где
 - подходит под второй специальный вид
- подходит под второй специальный вид 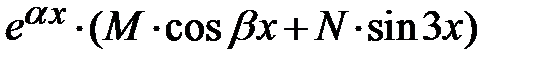 ,
,
 - подходит под первый специальный вид
- подходит под первый специальный вид  ;
;
в этом случае нужно использовать метод суперпозиции частных решений ЛНДУ, по которому частное решение  нужно искать в виде суммы двух функций
нужно искать в виде суммы двух функций 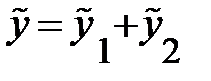 , где
, где
 - это частное решение ЛНДУ
- это частное решение ЛНДУ  ,
,
 - это частное решение ЛНДУ
- это частное решение ЛНДУ  .
.
Так как обе правые части  и
и  имеют специальный вид, то каждая из функций
имеют специальный вид, то каждая из функций 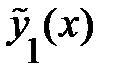 и
и  наиболее просто находятся методом неопределённых коэффициентов;
наиболее просто находятся методом неопределённых коэффициентов;
В соответствии с теоретическими рекомендациями:
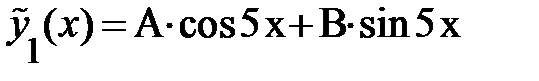 , так как
, так как  ,
,  = >
= >  ;
;
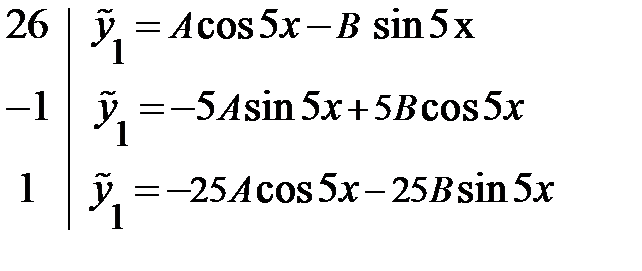
 <=>
<=>  <=>
<=>
 <=>
<=>  <=>
<=>  <=>
<=>  =>
=> 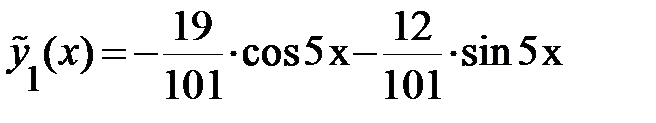 ;
;
Проверка  :
:


 , так как
, так как  =>
=>  ,
,  =>
=> 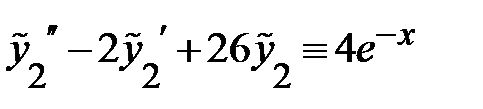
<=>  <=>
<=>  =>
=>
 (достоверность функции
(достоверность функции 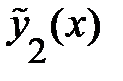 легко подтверждается проверкой);
легко подтверждается проверкой);
сложением найденных функций  и
и  определим функцию
определим функцию  :
:
 ;
;
4) определив функции  и
и 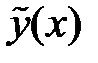 , составляем общее решение исходного ЛНДУ
, составляем общее решение исходного ЛНДУ 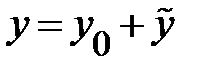 и упрощаем функцию
и упрощаем функцию 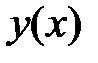 к лаконичному виду.
к лаконичному виду.
Ответ по задаче 1.6:
 .
.
Дата добавления: 2015-08-26; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 5 | | | Задание 2 |