|
Читайте также: |
Решить систему линейных ДУ: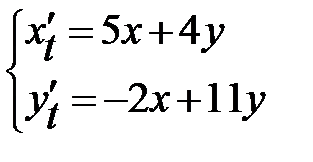 
Решение
Имеем систему двух обыкновенных ДУ первого порядка относительно функций 
и 
. Эти ДУ являются линейными и однородными. Реализуем решение системы методом исключения одной из функций; в результате получим ДУ более высокого порядка относительно другой функции.
Будем исключать функцию y, а х оставим:
1) первое уравнение системы дифференцируем по t:
;
2) подставляем 
, взятое из второго уравнения системы 
:
<=> 
;
3) берем у из первого уравнения системы 
и подставляем в равенство, полученное на предыдущем шаге:
<=> 
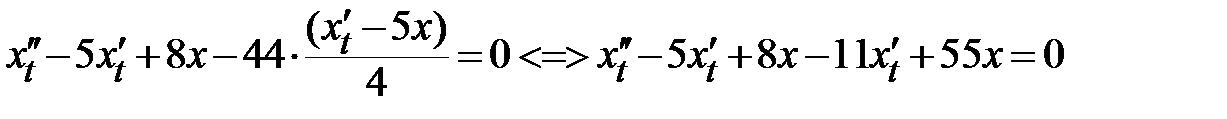- получено ДУ второго порядка относительно функции 
.
Находим функцию как общее решение получившегося ДУ второго порядка, тип которого определяется как ЛОДУ с постоянными коэффициентами:
=> 
;
характеристическое уравнение: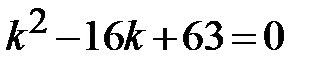 
<=> 
=>
, 
=> 
.
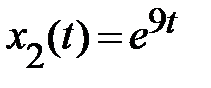Ищем вторую функцию , используя первое уравнение исходной системы 
и подставляя в него найденную функцию :
<=> 
.
Для проверки достоверности найденных функций и их следует подставить в оба уравнения исходной системы:
=> 
1-е уравнение: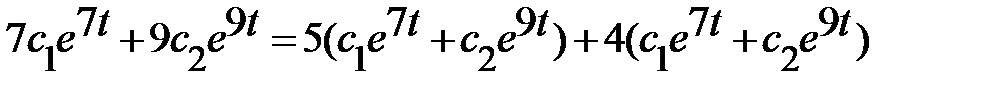 
<=>
- верно при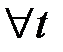 
, 
, 
;
2-е уравнение: 
<=>
- верно при , , ;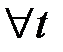
проверка показала, что общее решение данной системы найдено правильно.
Ответ по заданию 2:
Дата добавления: 2015-08-26; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 1 | | | Задание 3 |