
|
Читайте также: |
Построить интегральные линии данного дифференциального уравнения первого порядка. Найти уравнение интегральной линии, проходящей через точку  . Проанализировать теорему существования и единственности частных решений для данного ДУ:
. Проанализировать теорему существования и единственности частных решений для данного ДУ:

 .
.
Решение
Интегральные линии дифференциального уравнения – это графическое изображение общего решения ДУ;
для дифференциального уравнения первого порядка интегральные линии представляют собой однопараметрическое семейство линий  на плоскости XOY.
на плоскости XOY.
Поэтому находимобщее решение данного ДУ:  <=>
<=>
 <=>
<=> 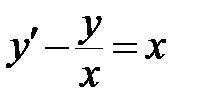 - линейное ДУ вида
- линейное ДУ вида  =>
=>
метод решения: 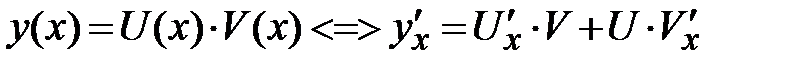 ;
;
ДУ:  <=>
<=>  <=>
<=> 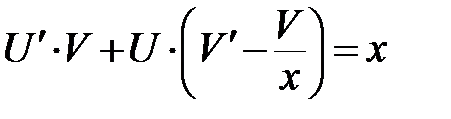 ;
;
ДУ для функции  <=
<= 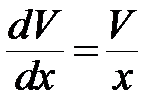 <=>
<=>  <=>
<=>  <=>
<=> 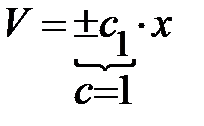 <=>
<=> 
ДУ для функции  <=>
<=> 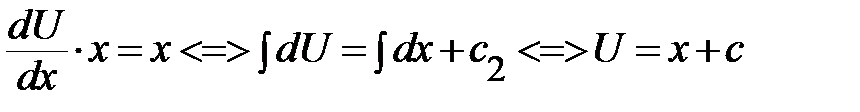 ;
;
общее решение исходного ДУ: 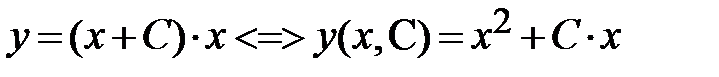 ;
;
геометрически общему решению соответствует семейство парабол, ветви которых направлены вверх и которые пересекают ось ОX в точках  и
и  .
.
Изменяя значения произвольной постоянной  , получим несколько интегральных линий данного ДУ (рис. 1):
, получим несколько интегральных линий данного ДУ (рис. 1):
если  , то
, то 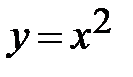 - парабола с вершиной
- парабола с вершиной 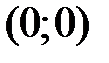 ;
;
если 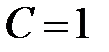 , то
, то  - парабола с вершиной
- парабола с вершиной  ;
;
если 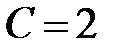 , то
, то  - парабола с вершиной
- парабола с вершиной  ;
;
если 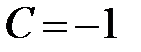 , то
, то  парабола с вершиной
парабола с вершиной 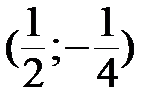 ;
;
заметим, что все параболы, имеющие уравнение  , проходят через начало координат.
, проходят через начало координат.
| x |
| y |
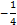
|

|
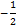
|

|

|

|
| -1 |
| -1 |

|
| Рис. 1 |
Находим интегральную линию, проходящую через точку  :
:
подставим  ,
,  в найденное общее решение и определим значение
в найденное общее решение и определим значение  , соответствующее начальному условию
, соответствующее начальному условию  :
:
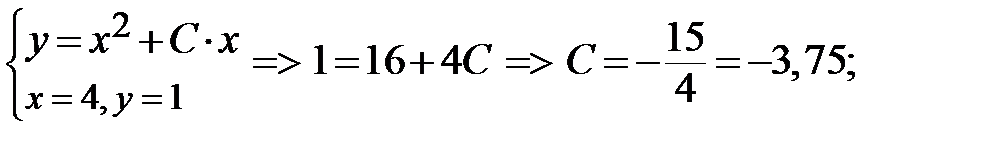
| x |
| y |

|
| 3,75 |
| 1,875 |
| -3,5 |
| Рис. 2 |
| M 0(4;1) |
 общее решение, получим частное решение данного ДУ, соответствующее поставленному начальному условию:
общее решение, получим частное решение данного ДУ, соответствующее поставленному начальному условию:  . Геометрически ему соответствует парабола с вершиной в точке
. Геометрически ему соответствует парабола с вершиной в точке
(1,875;-3,5) и проходящая через очку M 0(4;1), которая изображена на рисунке 2.
Проанализируем теорему существования и единственности частных решений для данного ДУ первого порядка. Для этого сначала сформулируем эту теорему:
Если
1) дано ДУ 1-го порядка, записанное в канонической форме  ,
,
2) дана фиксированная точка 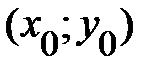 , которой соответствует начальное условие
, которой соответствует начальное условие 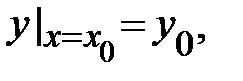
3) функции 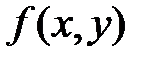 и
и  непрерывны в точке
непрерывны в точке 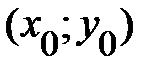 ,
,
то существует единственное частное решение ДУ, удовлетворяющее данному начальному условию, то есть существует единственная интегральная линия ДУ, проходящая через точку 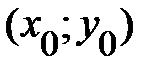 .
.
Проанализируем на непрерывность функции 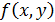 и
и 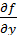 для данного ДУ:
для данного ДУ:
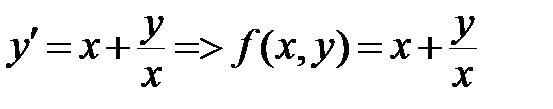 ,
, 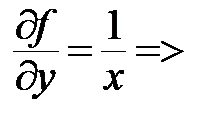
обе функции непрерывны для всех точек  , кроме тех точек, в которых
, кроме тех точек, в которых  . По теореме существования и единственности заключаем, что:
. По теореме существования и единственности заключаем, что:
1) через каждую точку  , у которой
, у которой 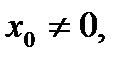 проходит единственная интегральная линия данного ДУ;
проходит единственная интегральная линия данного ДУ;
2) точки  не удовлетворяют теореме существования и единственности, поэтому они являются особыми точками для данного ДУ; через каждую из этих точек может проходить или несколько интегральных линий, или ни одной, но может быть и одна интегральная линия.
не удовлетворяют теореме существования и единственности, поэтому они являются особыми точками для данного ДУ; через каждую из этих точек может проходить или несколько интегральных линий, или ни одной, но может быть и одна интегральная линия.
В данной задаче через особую точку  проходят все интегральные линии, через остальные точки
проходят все интегральные линии, через остальные точки  , у которых
, у которых  , не проходит ни одна интегральная линия.
, не проходит ни одна интегральная линия.
Ответ по задаче 3:
1) 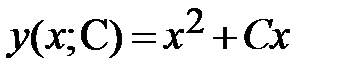 - уравнение множества интегральных линий ДУ
- уравнение множества интегральных линий ДУ 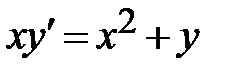 ; интегральные линии построены на Рис. 1;
; интегральные линии построены на Рис. 1;
2) 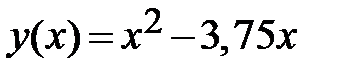 - уравнение интегральной линии, проходящей через точку
- уравнение интегральной линии, проходящей через точку  ; эта линия построена на Рис. 2;
; эта линия построена на Рис. 2;
3) в результате анализа теоремы существования и единственности частных решений получено, что через каждую точку 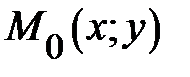 , у которой
, у которой  , проходит единственная интегральная линия;
, проходит единственная интегральная линия;
точки вида  , заполняющие полностью ось OY, являются особыми точками данного ДУ.
, заполняющие полностью ось OY, являются особыми точками данного ДУ.
Дата добавления: 2015-08-26; просмотров: 256 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 2 | | | Задание 4 |