
Читайте также:
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
ФГБОУ ВПО «Мурманский государственный технический университет»
Кафедра ВМ и ПО ЭВМ
Расчетно-графическое задание
«Обыкновенные ДУ и системы ДУ»
по дисциплине «Специальные разделы высшей математики»
выполнил: студент группы ИВТ(б)-211(1)
Сумин И.А.
проверил: доцент кафедры
Кацуба В.С.
оценка: _____________________
дата: _____________________
Мурманск
Приложение Б. Варианты заданий
Задание 1. Определить тип обыкновенного дифференциального уравнения, найти его общее решение и найти частное решение, если поставлены начальные условия.
| № вар. | Диф. уравнения 1.1, 1.2, 1.3. | Диф. уравнения 1.4, 1.5, 1.6 |
1.1.  , ,  ;
1.2. ;
1.2. , , 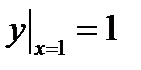 ;
1.3. ;
1.3.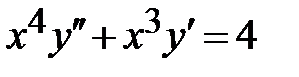 ; ;
| 1.4.  , , 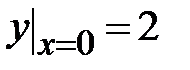 , ,  ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 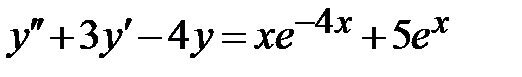
| |
1.1. 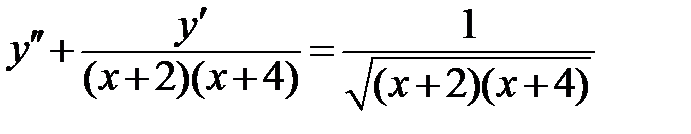  ;
1.2. ;
1.2.  , ,  , , 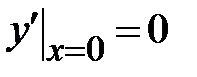 ;
1.3. ;
1.3. ; ;
| 1.4.  , ,  , ,  ;
1.5. ;
1.5. 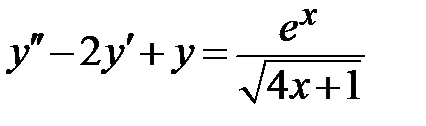 ;
1.6. ;
1.6.
| |
1.1.  , ,  ;
1.2. ;
1.2. ;
1.3. ;
1.3. 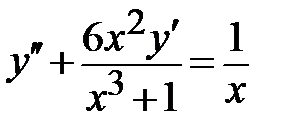 ; ;
| 1.4.  , ,  , ,  ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 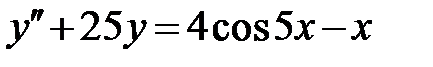  
| |
1.1.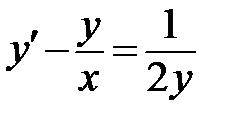 ;
1.2. ;
1.2. , , 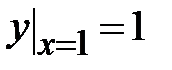 ;
1.3. ;
1.3. 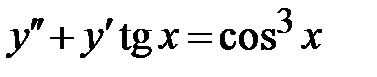 ; ;
| 1.4.)  , ,  , , 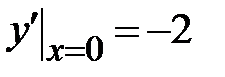 ;
1.5. ;
1.5. 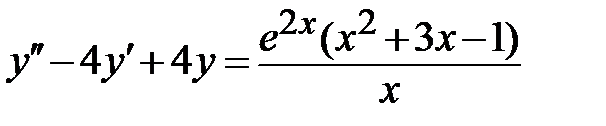 ;
1.6. ;
1.6.   
| |
1.1.  , , 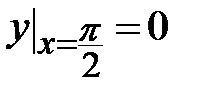 ;
1.2. ;
1.2.  ;
1.3. ;
1.3. 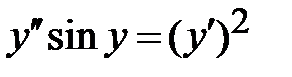 ; ;
| 1.4. 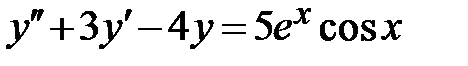 , , 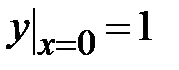 , ,  ;
1.5. ;
1.5. ;
1.6. ;
1.6. 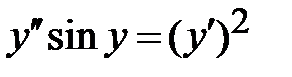
| |
1.1. 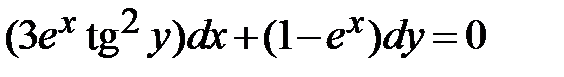 ;
1.2. ;
1.2.  , , 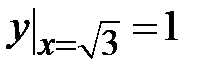 ;
1.3. ;
1.3. 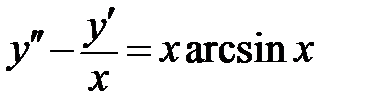   ; ;
| 1.4. 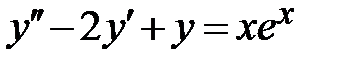 , ,  , , 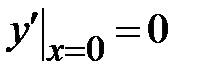 ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 
| |
1.1. ;
1.2. ;
1.2.  , , 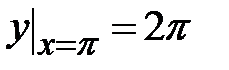 ;
1.3. ;
1.3.  ; ;
| 1.4. 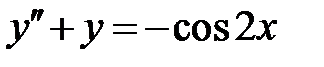 , ,  , ,  ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 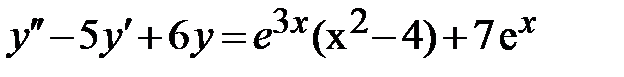
| |
1.1.  ;
1.2. ;
1.2.  , ,  ;
1.3. ;
1.3.  ; ;
| 1.4.  , ,  , , 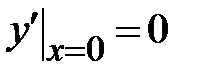 ;
1.5. ;
1.5. ;
1.6. ;
1.6. 
| |
1.1. , ,  ;
1.2. ;
1.2.  , , 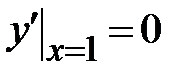 ;
1.3. ;
1.3. 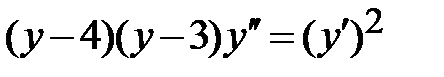 ; ;
| 1.4. 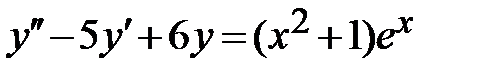 , ,  , ,  ;
1.5. ;
1.5.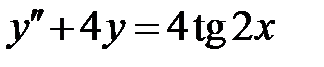 ;
1.6. ;
1.6. 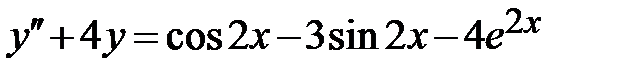
| |
1.1. , , 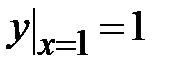 ;
1.2. ;
1.2. , , 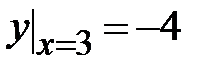 ;
1.3. ;
1.3.  , ,  , ,  ; ;
| 1.4.  ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 
| |
1.1. , , 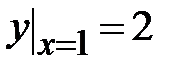 ;
1.2. ;
1.2. ;
1.3. ;
1.3.  , , 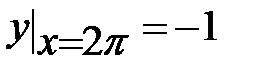 , ,  ; ;
| 1.4. 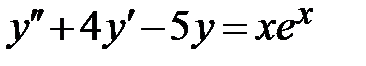 , , 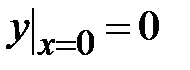 , , 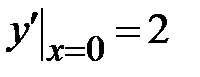 ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 
| |
1.1.  ;
1.2. ;
1.2. , , 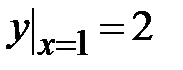 ;
1.3. ;
1.3.  , ,  , ,  ; ;
| 1.4.  , , 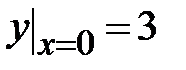 , , 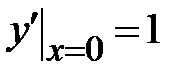 ;
1.5. ;
1.5.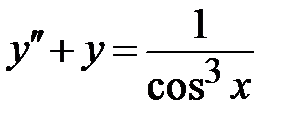 ;
1.6. ;
1.6. 
| |
1.1.  ;
1.2. ;
1.2. , , 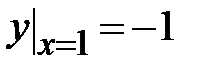 ;
1.3. ;
1.3. , , 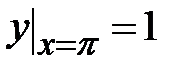 , , 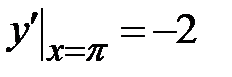 ; ;
| 1.4.  , ,  , , 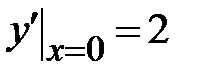 ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 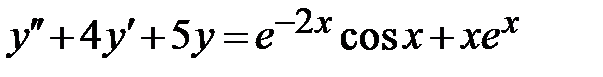
| |
1.1. , ,  ;
1.2. ;
1.2.  ;
1.3. ;
1.3. , ,  , ,  ; ;
| 1.4.  , ,  , ,  ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 
| |
1.1. , ,  ;
1.2. ;
1.2.  ;
1.3. ;
1.3.  , ,  , ,
 ; ;
| 1.4. 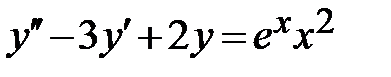 , ,  , , 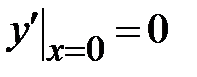 ;
1.5. ;
1.5.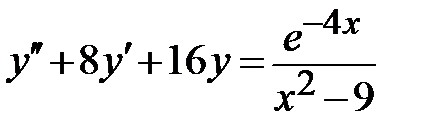 ;
1.6. ;
1.6. 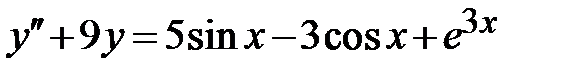 ; ;
| |
1.1. , ,  ;
1.2. ;
1.2. 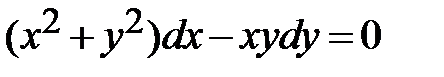 ;
1.3. ;
1.3.  ; ;
| 1.4.  , , 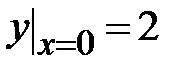 , ,  ;
1.5. ;
1.5. ;
1.6. ;
1.6.  , ,  , , 
| |
1.1. 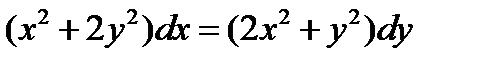 , ,  ;
1.2. ;
1.2. , ,  ;
1.3. ;
1.3.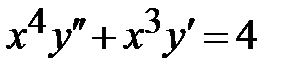 ; ;
| 1.4.  , , 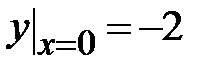 , ,  ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 
| |
1.1.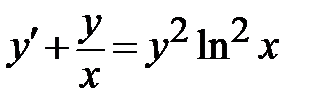 , ,  ;
1.2. ;
1.2. ;
1.3. ;
1.3. 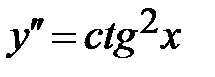 , ,  , ,  ; ;
| 1.4. 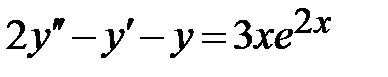 , ,  , ,  ;
1.5. ;
1.5.  ;
1.6. ;
1.6. 
| |
1.1. , ,  ;
1.2. ;
1.2. , , 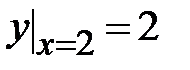 ;
1.3. ;
1.3.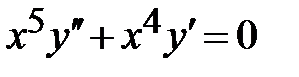 ; ;
| 1.4. 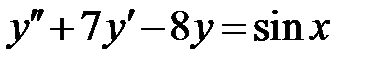 , ,  , ,  ;
1.5. ;
1.5. 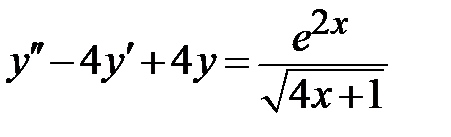 ;
1.6. ;
1.6. 
| |
1.1. , , 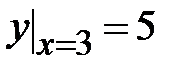 ;
1.2. ;
1.2. , , 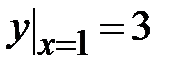 ;
1.3. ;
1.3.  , ,  , ,  ; ;
| 1.4. 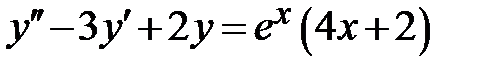 ;
1.5. ;
1.5. 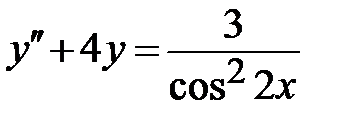 ;
1.6. ;
1.6. 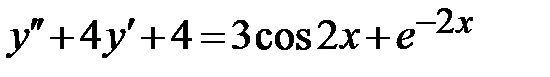
|
Задание 2. Решить систему линейных дифференциальных уравнений.
Задание 3. Построить интегральные линии дифференциального уравнения первого порядка. Найти уравнение интегральной линии, проходящей через заданную точку М 0. Проанализировать теорему существования и единственности частных решений для данного ДУ.
| № Варианта | Задание 2 | Задание 3 | ||

| 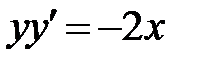 , , 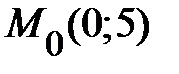
| |||
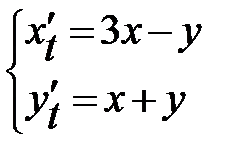
| 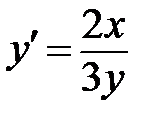 , , 
| |||

|  , ,  . .
| |||

|  , , 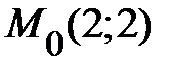 . .
| |||

|  , , 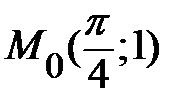 . .
| |||

|  , ,  . .
| |||

| 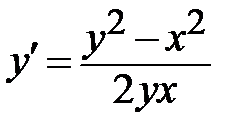 , ,  . .
| |||
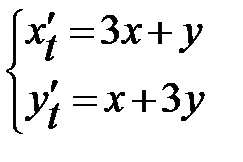
|  , , 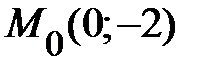 . .
| |||
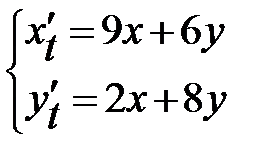
| 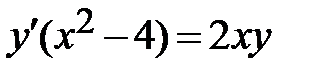 , ,  . .
| |||

|  , ,  . .
| |||

|  , ,  . .
| |||

| 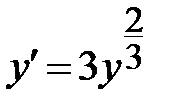 , ,  . .
| |||

| 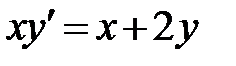 , ,  . .
| |||

|  , , 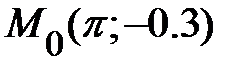 . .
| |||

|  , ,  . .
| |||

|  , ,  . .
| |||

|  , ,  . .
| |||

|  , , 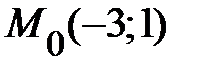 . .
| |||

| 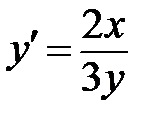 , , 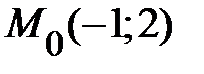 . .
| |||

|  , ,  . .
|
Задание 4. Решить задачу на определение уравнения линии по описанию её геометрических свойств, относящихся к её дифференциальным элементам.
| № вар. | Условие задачи |
| 1, 4, 7, 10, 13, 16, 19. | Найти все линии, у которых отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечение с осью ординат. (№3919, Берман) |
| 2, 5, 8, 11, 14, 17, 20. | Найти линию, у которой площадь трапеции, образованной осями координат, ординатой произвольной точки и касательной в этой точке, равна половине квадрата абсциссы. (№4007, Берман) |
| 3, 6, 9, 12, 15, 18. | Найти линию, обладающую следующим свойством: угол, составляемый с осью Ox касательной к линии в любой её точке, вдвое больше угла, который составляет с той же осью полярный радиус точки касания. (№4013, Берман) |
Задание 5. Физическая задача на движение (составление математической модели в виде обыкновенного ДУ, разрешение математической модели, интерпретация результатов).
Дата добавления: 2015-08-26; просмотров: 75 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решим составленную математическую модель | | | УМЗ-4215 |