
|
Читайте также: |
Найти линию, у которой любая касательная пересекается с осью ординат в точке, одинаково удаленной от начала координат и от точки касания.
Решение
Произведем разбор условия задачи
| x |
| y |
| M(x;y) – текущая точка искомой линии |
| А |
| касательная к искомой линии |
А – точка пересечения с осью ординат касательной, проведенной в произвольно выбранной точке (х,у) искомой линии.
По условию задачи |AM|=|AO| для любой точки M (x,y) искомой линии.
Требуется найти линию в виде её уравнения у = у (х) или F (х,у) = 0.
Составим математическую модель к данной задаче:
Искомую функцию у = у(х) нужно находить из условия |AM|=|AO| => надо составить уравнение касательной к линии и находить координаты её точки А.
Используем теоретическое уравнение касательной к линии y=y (x) в её фиксированной точке М (x0,y0):
| x |
| y |
| (x0,y0) |
| (х,у) |
y-y0=у’x (х0)  (х-х0) (х-х0)
|
| (х0,у0) – точка касания (х,у) – текущая точка на касательной |
| y=у (х) |
В решаемой задаче уравнение касательной запишем в следующем виде:
.  , где
, где
( ) – координаты точки касания;
) – координаты точки касания;
( ) – текущая точка на касательной.
) – текущая точка на касательной.
Для нахождения ординаты точки А нужно в уравнении касательной положить  и
и  , в результате получим:
, в результате получим: 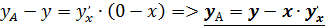 .
.
Расстояние |AM| и |AO| найдем по известной формуле для расстояния между двумя точками на плоскости:
|AM| =  => |АМ|=
=> |АМ|=  =
=  ;
;
|AO| = 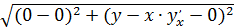 =
=  ;
;
| AM |=| AO | => | AM |2=| AO |2 =>  .
.
Таким образом, математической моделью решаемой задачи является составленное дифференциальное уравнение 1-го порядка относительно функции 
Требуется найти общее решение этого ДУ.
Дата добавления: 2015-08-26; просмотров: 193 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 3 | | | Решим составленную математическую модель |