Замечание

1) полный резерв времени работы равен резерву max из путей, проходящих через данную работу этим резервом можно располагать при выполнении данной работы, если ее начальное событие свершилось в свой ранний срок и можно допустить свершение конечного события в самый поздний срок.

2) полный резерв времени работы принадлежит не только этой работе, но и всем полным путям, проходящим через нее.

Частные резерв времени 1ого вида R₁ (I,j) есть часть полного резерва времени на которую можно увеличить продолжительность работы, не изменив при этом полного срока ее начального события.

R (i,j) = t_n(j) – t_n(i) – t(i,j)

R_i (i,j) = R_n (I,j) - R (i)

Свободный резерв времени R_c (i,j) есть часть полного резерва времени на которое можно увеличить время выполнения работы, не изменив при этом раннего срока свершения ее конечных событий. Этим резервом можно располагать при выполнении данной работы предполагая, что ее начальные и конечные события совершаются в свои ранние сроки.

R_i (i,j) = = t_р(j) – t_р(i) – t(i,j)

R_с (i,j) = R_n (I,j) - R (j)

Замечание:

Свободным резервом времени можно пользоваться для предотвращения случайностей, которые могут возникнуть при выполнении работ.

Независимый резерв времени R_н (I,j) часть полного резерва времени, получаемая для случая когда все предшествующие работы заканчиваются в поздние сроки, а все последние начинаются в ранние.

R_н(I,j) = R_n– R(i) – R(j)

R_н(I,j) = t_p(j) – t_n(i) – t(I,j)

Замечание:

Фактически независимый резерв имеют лишь те работы, которые лежат на max путях, проходят через их начальное и конечное события.

Общее замечание:

1) резервы времени работ (i, j) могут состоять из 2х временных отрезком, если интервал занимает промежуточную позицию.

2) частный резерв 1ого вида может быть использован на увеличение продолжительности данной и последующей работ. Rc используется для увеличения продолжительности данной и предшествующих работ. Rн используется для увеличения продолжительности данной работы.

3) работы, лежащие на критическом пути, резервов времени не имеют.

С помощью критических работ может быть определен критический путь сетевого графика. Если на критическом пути лежит начальное событие i, то полный резерв времени Rn (I,j) = Ri (i,j)

Нахождение кратчайшего пути

Пусть задана сеть из n + 1 вершины, то есть ориентированный граф, в котором выделены две вершины - вход (нулевая вершина) и выход (вершина с номером n). Для каждой дуги заданы числа, называемые длинами дуг. Длиной пути (контура) называется сумма длин входящих в него дуг (если длины дуг не заданы, то длина пути (контура) определяется как число входящих в него дуг). Задача заключается в поиске кратчайшего пути (пути минимальной длины) от входа до выхода сети.

Введем обозначения:

Dij — расстояние на сети между смежными узлами I и J;

Uj — кратчайшее расстояние между узлами I и J, U 1 = 0.

Формула для вычисления Uj:

Из формулы следует, что кратчайшее расстояние Uj до уз­ла J можно вычислить лишь после того, как определено крат­чайшее расстояние до каждого предыдущего узла I, соединен­ного дугой с узлом J. Процедура завершается, когда получено Ui последнего звена.

Определить кратчайшее расстояние между узлами 1 и 7

Решение. Найдем минимальные расстояния:

Минимальное расстояние между узлами 1 и 7 равно 13, а соответствующий маршрут: 1-2-5-7.

Минимизация сети

Задача минимизации сети состоит в нахождении ребер, со­единяющих все узлы сети и имеющих минимальную суммар­ную длину

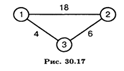
На ребрах, соединяющих узлы 1, 2, 3, указаны длины. Узел 3 соединен с узлами 1 и 2 минимальной длиной 4 + 6 = 10. Если соединить узлы 1 и 2, то возникает цикл и получающаяся сеть не будет минимальной. Отсутствие циклов в минимальной сети дало ей название "минимальное дерево-остов".

Начнем с любого узла и соединим его с ближайшим уз­лом сети. Соединенные два узла образуют связное множество, а остальные — несвязное. Далее в несвязном множестве выбе­рем узел, который расположен ближе других к любому из узлов связного множества. Скорректируем связное и несвязное мно­жества и будем повторять процесс до тех пор, пока в связное множество не попадут все узлы сети. В случае одинаково уда­ленных узлов выберем любой из них, что указывает на неодно­значность (альтернативность) "минимального дерева-остова".

Задача:

Телевизионная фирма планирует создание кабель­ной сети для обслуживания 5 районов-новостроек. Числа на ребрах указывают длину кабеля (рис. 30.18). Узел 1 — телеви­зионный центр. Отсутствие ребра между двумя узлами означа­ет, что соединение соответствующих новостроек либо связано с большими затратами, либо невозможно.

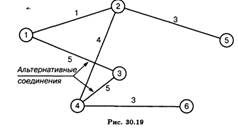
Найти такое соединение кабелем районов-новостроек, что­бы длина его была минимальной.

Решение. Минимальная длина кабеля: 1 + 3 + 4 + 3 + 5 = 16 (рис. 30.19).

Вопрос 20.Теория игр. Основные понятия.

Теория игр служит для моделирования оценки воздействия принятого решения на конкурентов.

Конфликтная ситуация, в которой 2 или более стороны преследуют различные цели, а результаты любого действия каждой из сторон зависит от мероприятий партнера. Игра - упрощенная формализованная математическая модель конфликтной ситуации. Игроки - стороны, участвующие в конфликте. Выигрыш (проигрыш) - исход конфликта. Правила игры - система условий, определяющих: 1)варианты возможных действий игроков, 2)величину выигрыша (проигрыша), 3) объем информации каждого игрока по поведению партнера. Парная игра - игра, в которой принимают участие 2 игрока. Множественная игра - игра, в которой принимают участие более двух игроков. Ход игрока – выбор и осуществление одного из предусмотренных правилами действий. Личный ход - сознательный выбор игроком одного из возможных действий. Случайный ход - случайный выбор…. Стратегия – совокупность правил определенного поведения игрока при каждом личном ходе в зависимости от сложившейся ситуации. Решение игры – пара стратегий при которой 1 из игроков должен получить максимальный выигрыш, когда второй придерживается своей стратегии, в то же время второй игрок должен иметь минимальый проигрыш.

Матричные игры.

Матричная игра двух игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков.

Первый игрок имеет m стратегий i = 1,2,...,m, второй имеет n стратегий j = 1,2,...,n. Каждой паре стратегий (i,j) поставлено в соответствие число аij, выражающее выигрыш игрока 1 за счёт игрока 2, если первый игрок примет свою i-ю стратегию, а 2 – свою j-ю стратегию. Каждый из игроков делает один ход: игрок 1 выбирает свою i-ю стратегию (i=1,m), 2 – свою j-ю стратегию (j=1,n), после чего игрок 1 получает выигрыш аij за счёт игрока 2 (если аij< 0, то это значит, что игрок 1 платит второму сумму | аij |). На этом игра заканчивается. Каждая стратегия игрока (i=1,m); (j =1,n) часто называется чистой стратегией. Если рассмотреть матрицу

|a11 a12 … a1j … a1n|

А = | ai1 ai2 … aij … ain |

|am1 am2 … amj … amn|

то проведение каждой партии матричной игры с матрицей ^ А сводится к выбору игроком 1 i-й строки, а игроком 2 j-го столбца и получения игроком 1 (за счёт игрока 2) выигрыша аij. Главным в исследовании игр является понятие оптимальных стратегий игроков. В это понятие интуитивно вкладывается такой смысл: стратегия игрока является оптимальной, если применение этой стратегии обеспечивает ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока. Исходя из этих позиций, игрок 1 исследует матрицу выигрышей А следующим образом: для каждого значения i (i =1,m) определяется минимальное значение выигрыша в зависимости от применяемых стратегий игрока 2

minjaij(i=1,m)

т.е. определяется минимальный выигрыш для игрока 1 при условии, что он примет свою i-ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i = iо, при которой этот минимальный выигрыш будет максимальным, т.е. находится

maxiаij =ai0j0 = α (1).

Определение. Число α, определённое по формуле (1) называется нижней чистой ценой игры и показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2.

Игрок 2 при оптимальном своём поведении должен стремится по возможности за счёт своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 отыскивается

maxiаij

т.е. определяется max выигрыш игрока 1, при условии, что игрок 2 применит свою j-ю чистую стратегию, затем игрок 2 отыскивает такую свою j = j1 стратегию, при которой игрок 1 получит min выигрыш, т.е. находит

min j maxi aij =ai1j1 =α (2).

Определение. Число α, определяемое по формуле (2), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счёт своих стратегий может себе гарантировать игрок 1. Другими словами, применяя свои чистые стратегии игрок 1 может обеспечить себе выигрыш не меньше α, а игрок 2 за счёт применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем α.Определение. Если в игре с матрицей А α = α, то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры

Седловая точка – это пара чистых стратегий (iо,jо) соответственно игроков 1 и 2, при которых достигается равенство α = α. В это понятие вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Математически это можно записать и иначе:

Aij0 ≤ ai0j0 ≤ ai0j (3)

где i, j – любые чистые стратегии соответственно игроков 1 и 2; (iо,jо) – стратегии, образующие седловую точку.

Таким образом, исходя из (3), седловой элемент является минимальным в iо-й строке и максимальным в jо-м столбце в матрице А. Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своём столбце. Если да, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий (iо,jо) игроков 1 и 2, образующая седловую точку и седловой элемент ai0j0, называется решением игры. При этом iо и jо называются оптимальными чистыми стратегиями соответственно игроков 1 и 2.

Вопрос 22.

Смешанные стратегии матричных игр.

Теорема матричных игр.

Смешанные стратегии. Дальнейшее развитие теории матричных игр основывается на исследовании игры как некоторого повторяющегося процесса. Действительно, вряд ли можно дать содержательные рекомендации по такому вопросу, как следует поступать участникам однократно проводимой игры, не имеющей седловой точки. В случае же ее многократных повторов естественной и плодотворной представляется идея рандомизации выбора стратегий игроками, т. е. внесение в процесс выбора элемента случайности. Действительно, систематическое отклонение, например, игрока I от максиминной стратегии с целью увеличения выигрыша может быть зафиксировано вторым игроком и наказано. В то же время абсолютно хаотичный выбор стратегий не принесет в среднем наилучшего результата.

F Смешанной стратегией игрока I в игре с матрицей A =║ a_i,j ║ _{m x n} называется упорядоченный набор действительных чисел x_i, i ∊1: m, удовлетворяющих условиям

Числа интерпретируются как вероятности применения игроком I стратегий 1, 2,..., m, которые, в отличие от смешанных, также называют чистыми стратегиями.

Аналогично вводится понятие смешанных стратегий игрока II, которые определяются как набор чисел у_j, j ∊1: n, удовлетворяющих условиям

Тогда, если игрок I применяет смешанную стратегию х = (х ₁, х ₂,..., х_m) а игрок II смешанную стратегию y = (y ₁, y ₂,..., y_n), то математическое ожидание выигрыша игрока I (проигрыша игрока II) определяется соотношением

*

* Напомним, что при многократном повторении игры средний выигрыш близок к математическому ожиданию.

В дальнейшем через Х будем обозначать множество допустимых смешанных стратегий игрока I, определяемое условием 6.7, а через Y — определяемое условием 6.8 множество допустимых смешанных стратегий игрока II.

К поиску решения игры в смешанных стратегиях, так же как и в п. 6.1.3, могут быть применены критерии максимина-минимакса. В соответствии с ними игрок I будет выбирать свою смешанную стратегию х = (х ₁, х ₂,..., х_m) таким образом, чтобы максимизировать наименьший средний выигрыш:

который, как можно доказать, равен

а игрок II — свою смешанную стратегию так, чтобы минимизировать наибольший средний проигрыш:

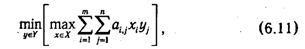
также равный

По аналогии с (6.3) для любых х ∊ Х и y ∊ Y справедливо неравенство

F Стратегии х* ∊ Х и y* ∊ Y называют оптимальными смешанными стратегиями, если для любых х ∊ Х и y ∊ Y справедливо равенство

v =F (x*, у*) называют ценой игры, и если х* и у* существуют, то говорят, что игра имеет решение в смешанных стратегиях (х*, у*, v).

Справедлива фундаментальная теорема Дж. Неймана, которую мы приведем без доказательства.

Теорема 6.1 (основная теорема матричных игр). Любая матричная игра имеет решение в смешанных стратегиях.

Или в игре имеется седловая точка, т. е. выполнено условие. Или иначе, любая матричная игра имеет седловую точку в смешанных стратегиях.
Доказательство этой теоремы основано на теории множеств.
Заметим только, что множество оптимальных смешанных стратегий оперирующей стороны (равно как и противника в антагонистической игре) является выпуклым и замкнутым.

Значение и нетривиальность теоремы (6.1) обусловлены прежде всего тем, что, как было показано в п. 6.1.3, в общем случае матричные игры в чистых стратегиях решения не имеют.

Вопрос 23.

графическое решение игры 2х2.

Для графического решения системы уравнений отложим по оси абсцисс вероятность q₁Î[0,1], а по оси ординат соответствующие этой вероятности выигрыши игрока В:

v =(a₁₁-a₁₂)q₁+a₁₂; (2.23)

v =(a₂₁-a₂₂)q₁+a₂₂ (2.24)

Рис. 2.5.

Решением являются координат точки М пересечения прямых, описываемых уравнений (2.23) и (2.24):

q_1opt:q_2opt=1-q_1opt и v _opt

Это же следует и из принципа максимина, в соответствии с которым игрок В должен выбрать такую смешанную стратегию, при которой его максимальный проигрыш будет минимами.

Для игры G(2х2) с седловой точкой геометрическая интерпретация решения быть представлена, например, следующим образом (рис.2.6.)

Рис. 2.6.

Стратегия В ₂ игрока В является для него явно невыгодной, так как, применяя ее, он в любой случае проигрывает больше, чем при применении стратегии В ₁. В данной игре р_1opt=1;р_2opt=0; v _opt=а₁₁, т.е. игра имеет седловую точку N и решается в чистых стратегиях. Игрок А должен применять стратегию А ₁, а игрок В - стратегию В₁.

На рис. 2.7 показан случай, в котором решением игры для игрока А является чистая стратегия А ₂, а для игрока В - стратегия В ₁.

Рис. 2.7

Игра имеет седловую точку N.

Пример: Найти алгебраическим и геометрическим методами решение игры, платежная матрица которой имеет вид

Bj   Ai	B1	B2	a i
A1		-2	-2
A2
b j

В данной игре нижняя цена игры a=1 не равна верхней цены игры b=3, поэтому игра не имеет седловой точки и, в соответствии с основной теоремой матричных игр, имеет оптимальное решение в смешанных стратегиях.

Для игрока А, в соответствии с формулами (2.15) и (2.16), оптимальные вероятности применения стратегий А₁ и А₂ равны:

Для игрока В, в соответствии с формулами (2.20) и (2.21), оптимальные вероятности применения стратегий В₁ и В₂ равны:

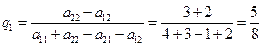
Таким образом, оптимальные смешанные стратегии игроков ; , а цена игры в соответствии с формулой (2.22) равна:

Так как n >0, то игра выгодна для игрока А.

Графическое изображение игры для игрока А показана на рис. 2.8.

Рис. 2.8

Нижняя граница выигрыша игрока А определяется ломаной CND. Оптимальное решение, определяется точкой N, естественно, дает тоже решение, что и алгебраический метод: .

Географическое изображение игры для игрока В показана на рис.2.9.

Рис. 2.9.

Оптимальное решение определяемое точкой М, дает решение .

Дата добавления: 2015-08-20