Простейшая задача о рационе.

Введение

Данная работа посвящена решению задач линейной алгебры в Excel,точнее решению систем линейных уравнений. Будут рассмотрены три метода: метод Гаусса, метод, основанный на нахождении обратной матрицы и метод наименьших квадратов.

В первом параграфе работы в качестве примера использования систем линейных уравнений в экономике приведена простейшая задача о рационе и её решение методом Гаусса в частном случае, когда количество неизвестных совпадает с количеством уравнений.

Во втором параграфе рассматривается модель Леонтьева межотраслевого баланса. Это модель, позволяющая анализировать состояние экономики и моделировать различные сценарии ее развития. Возникающая в этом методе система линейных уравнений традиционно решается нахождением обратной матрицы. Чтобы пояснить, запишем модель Леонтьева в матричной форме:

(E-A)*X=Y

Если у нас имеется матрица (Е-А)^-1 ,то умножая обе части равенства на эту матрицу, получим: Х=(Е-А)^-1*У.

Третий параграф описывает решение задач, сводящихся к решению систем линейных уравнений, при помощи МНК (метода наименьших квадратов).

В каждом параграфе будет приведена реализация в Excel.

Метод Гаусса и одно из его приложений в экономике (задача о рационе).

Простейшая задача о рационе.

Формулировка задачи. Допустим, на ферме занимаются выращиванием телят. Известно, что для хорошего роста теленка в день ему необходимо потреблять m веществ в количестве 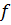,…, соответственно.

На ферму ежедневно завозится n кормов в количестве 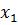,…, . Известно, что доля итогового вещества в j -ом корме равна . Тогда общее количество вещества

определяется по формуле

=

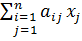
(слагаемое - количество итогового вещества в j корме; i =1,…,n).

В результате получаем систему

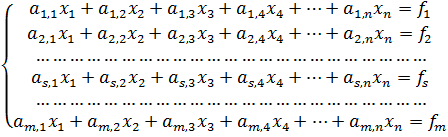(1)

Если m ≠ n,то система называется прямоугольной и методы её решения рассматриваются в другом параграфе. В данном случае будем считать, что m=n. Такая система является квадратной и к ней применим метод Гаусса.

Дата добавления: 2015-08-20